Kinh Nghiệm Hướng dẫn Đường thẳng y = ax 2 trải qua điểm A 1 5 thi Chi Tiết
Quý khách đang tìm kiếm từ khóa Đường thẳng y = ax 2 trải qua điểm A 1 5 thi được Cập Nhật vào lúc : 2022-10-23 21:35:23 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Sách Giải Sách Bài Tập Toán 9 Bài 2: Đồ thị hàm số y = ax (a ≠ 0) giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 9 sẽ hỗ trợ bạn rèn luyện kĩ năng suy luận hợp lý và hợp logic, hình thành kĩ năng vận dụng kết thức toán học vào đời sống và vào những môn học khác:
a. Vẽ đồ thị hàm số.
b. Các điểm sau có thuộc đồ thị hay là không : A(3; 0,9), B(-5; 2,5), C(-10; 1)?
Lời giải:
a. Các giá trị của x và y :
x -5 -3 0 3 5 y = 0,1x2 2,5 0,9 0 0,9 2,5
b. *Thay hoành độ điểm A vào phương trình hàm số :
y = 0,1.32 = 0,9 = yA
Vậy điểm A(3; 0,9) thuộc đồ thị hàm số.
*Thay hoành độ điểm B vào phương trình hàm số :
y = 0,1.(-5)2 = 2,5 = yB
Vậy điểm B(-5; 2,5) thuộc đồ thị hàm số.
*Thay hoành độ điểm C vào phương trình hàm số :
y = 0,1.(-10)2 = 10 ≠ yC
Vậy điểm C(-10; 1) không thuộc đồ thị hàm số.
a. Đồ thị của nó trải qua điểm A(3 ; 12) ;
b. Đồ thị của nó trải qua điểm B(-2 ; 2).
Lời giải:
a. Đồ thị hàm số y = ax2 trải qua điểm A(3 ; 12) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có : 12 = a.32 ⇔ a = 12/9 = 4/3
Vậy hàm số đã cho là y = (4/3) x2.
b. Đồ thị hàm số y = ax2 trải qua điểm B(-2 ; 3) nên tọa độ điểm B nghiệm đúng phương trình hàm số.
Ta có : 3 = a.(-2)2 ⇔ a = 3/4
Vậy hàm số đã cho là y = (3/4)x2
a. Biết rằng điểm A(-2 ;b) thuộc đồ thị, hãy tính b. Điểm A’(2 ; b) có thuộc đồ thị hàm số không ? Vì sao ?
b. Biết rằng điểm C(c ; 6) thuộc đồ thị, hãy tính c. Điểm D(c ; -6) có thuộc đồ thị hàm số không ? Vì sao ?
Lời giải:
a. Đồ thị hàm số y = 0,2x2 trải qua điểm A(-2 ; b) nên tọa độ điểm A nghiệm đúng phương trình hàm số.
Ta có : b = 0,2.22 = 0,8
Điểm A(-2; b) thuộc đồ thị hàm số y = 0,2x2 mà điểm A’(2 ; b) đối xứng với điểm A(-2; b) qua trục tung nên điểm A’(2; b) thuộc đồ thị hàm số y = 0,2x2.
b. Đồ thị hàm số y = 0,2x2 trải qua điểm C(c; 6) nên tọa độ điểm C nghiệm đúng phương trình hàm số.
Ta có : 6 = 0,2.c2 ⇔ c2 = 6/(0,2) = 30 ⇒ c = ±√(30)
Điểm D(c; -6) đối xứng với điểm C(c; 6) qua trục hoành mà đồ thị hàm số y = 0,2x2 gồm hai nhánh đối xứng qua trục tung nên điểm C(c ; 6) thuộc đồ thị hàm số thì điểm D(c ; -6) không thuộc đồ thị hàm số.
a. Vẽ hai đồ thị của những hàm số này trên cùng một mặt phẳng tọa độ.
b. Tìm tọa độ giao điểm của hai đồ thị.
Lời giải:
a. *Các giá trị của x và y :
x -5 -3 0 3 5 y = 0,2x2 5 1,2 0 1,2 5*Đồ thị hàm số y = x trải qua gốc tọa độ O.
y = 0,2x2

b. Đồ thị của hai hàm số cắt nhau tại 2 điểm : O(0 ; 0) và A(5 ; 5).
a. Xác định thông số a biết rằng đồ thị của nó cắt đường thẳng y = -2x + 3 tại điểm A có hoành độ bằng 1.
b. Vẽ đồ thị của hàm số y = -2x + 3 và của hàm số y = ax2 với giá trị của a vừa tìm kiếm được trong câu a) trên cùng một mặt phẳng tọa độ.
c. Nhờ đồ thị, xác lập tọa độ của giao điểm thứ hai của đồ thị vừa vẽ trong câu b.
Lời giải:
a. Điểm A thuộc đồ thị hàm số y = -2x + 3 nên tọa độ A nghiệm đúng phương trình đường thẳng.
Ta có : y = -2.1 + 3 = 1
Vậy điểm A(1 ; 1)
Điểm A(1 ; 1) thuộc đồ thị hàm số y = ax2 nên tọa độ A nghiệm đúng phương trình hàm số.
Ta có : 1 = a.12 ⇔ a = 1
Vậy hàm số đã cho là y = x2
b. *Vẽ đồ thị hàm số y = x2
Các giá trị của x và y :

y = -2x + 3
x -3 -2 -1 0 1 2 3 y = 0,2x2 9 4 1 0 1 4 9*Vẽ đồ thị hàm số y = -2x + 3
Cho x = 0 thì y = 3 ⇒ (0 ; 3)
Cho y = 0 thì x = 1,5 ⇒ (1,5 ; 0)
c. Giao điểm thứ hai của đồ thị có hoành độ bằng -3 và tung độ bằng 9. Ta có : B(-3 ; 9).
a. Vẽ đồ thị của hàm số.
b. Tìm trên đồ thị điểm A có hoành độ bằng -2. Bằng đồ thị, tìm tung độ của A.
c. Tìm trên đồ thị những điểm có tung độ bằng 4. Tính gần đúng (làm tròn đến chữ số thập phân thứ nhất) hoành độ của những điểm này bằng hai cách :
– Ước lượng trên đồ thị ;
– Tính theo công thức

Lời giải:
a. Vẽ đồ thị hàm số
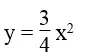
Các giá trị của x và y:
x -3 -2 0 2 3 y = 0,2x2 27/4 3 0 3 27/4b. Từ điểm có hoành độ x = -2, kẻ đường thẳng tuy nhiên tuy nhiên với trục tung cắt đồ thị tại điểm A. Từ A, kẻ đường thẳng tuy nhiên tuy nhiên với trục hoành cắt trục tung tại một điểm. Ta thấy điểm đó có tung độ y = 3.
Vậy A(-2 ; 3).
c. *Từ điểm có tung độ y = 4, kẻ đường thẳng tuy nhiên tuy nhiên với trục hoành cắt đồ thị hàm số tại hai điểm là B và B’. Cả hai điểm đều phải có tung độ y = 4.
Từ B và B’, kẻ hai tuyến phố thẳng tuy nhiên tuy nhiên với trục tung cắt trục hoành tại hai điểm có hoành độ lần lượt là x ≈ -2 và x ≈ 2.
*Thay y = 4 vào hàm số
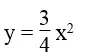
ta có :

a. Vẽ đồ thị của hàm số.
b. Không làm tính, dùng đồ thị để so sánh f(-1,5) và f(-0,5), f(0,75) và f(1,5)
c. Dùng đồ thị, tìm những giá trị thích hợp điền vào những chỗ (…) :
Khi 1 ≤ x ≤ 2 thì … ≤ y ≤ ….;
Khi -2 ≤ x ≤ 0 thì … ≤ y ≤ …;
Khi -2 ≤ x ≤ 1 thì ….≤ y ≤ …
Lời giải:
a. Vẽ đồ thị của hàm số y = -1,5x2
Các giá trị của x và y :
x -2 -1 0 1 2 y = 1,5x2 -6 -1,5 0 -1,5 -6
b. Hàm số y = -1,5x2 có a = -1,5 < 0
Vậy hàm số đồng biến trong mức chừng x < 0, nghịch biến trong mức chừng x > 0
Suy ra : f(-1,5) < f(-0,5), f(0,75) > f(1,5)
c. Ta có :
– Khi 1 ≤ x ≤ 2 thì -6 ≤ y ≤ -1,5 ;
– Khi -2 ≤ x ≤ 0 thì -6 ≤ y ≤ 0 ;
– Khi -2 ≤ x ≤ 1 thì -6 ≤ y ≤ 0.

– Đặt tờ giấy kính lên tờ giấy đã vẽ 5 đường tròn sao cho đường tròn (1) trải qua K và tiếp xúc với Ht và tâm I nằm bên cạnh phải Oy. Trên tờ giấy kính, ghi lại vào chỗ điểm I xuất hiện và kí hiệu là yếu tố A.
– Di chuyển tờ giấy kính sang trái sao cho đường tròn (2) trải qua K và tiếp xúc với Ht. Trên tờ giấy kính, ghi lại vào chỗ điểm I xuất hiện và kí hiệu là yếu tố B (xem hình dưới).
– Tiếp tục làm như vậy riêng với những đường tròn còn sót lại ta lần lượt được những điểm C, D, E trên tờ giấy kính.
– Lấy những điểm A’, B’, C’, D’, E’ lần lượt đối xứng với những điểm A, B, C, D, E qua Oy.
– Nối những điểm E’, D’, C’, B’, A’, A, B, C, D, E bởi một đường cong ta được một parabol.
Lời giải:
Học sinh thực thi theo phía dẫn.
A) 1
B) -1
C) 2
D) 1/2

Lời giải:
Parabol y = x2 trong hình vẽ có thông số a bằng
Chọn D) 1/2
Vì điểm có hoành độ x = 2 thì tung độ y = 2 nên:

a) Tìm những giá trị của x để y < 2.
b) Tìm những giá trị của x để y > 2.
c) Tìm những giá trị của y khi -2 < x < 2
d) Tìm những giá trị của y khi x ≤ 0.
e) Tìm những giá trị của y khi x ≤ 2.
Lời giải:
a) Để giá trị y < 2 thì -2 < x < 2
b) Để giá trị y > 2 thì x > 2 hoặc x < -2
c) Khi -2 < x < 2 thì 0 ≤ y ≤ 2
d) Khi x ≤ 0 thì y ≥ 0
e) Khi x ≤ 2 thì y ≥ 0
b) Xác định đường thẳng y = a’x + b’ biết rằng đường thẳng này cắt đồ thị của hàm số vừa tìm kiếm được trong câu a tại điểm A và điểm B có tung độ là 8.
Lời giải:
a) Đồ thị hàm số trải qua A (-1; 2) nên tọa độ của A nghiệm đúng phương trình hàm số: 2 = a(- 1)2} ⇔ a = 2
Hàm số đã cho: y = 2x2
Vẽ đồ thị hàm số: y = 2x2
x
-2
-1
0
1
2
y = 2x28
2
0
2
8

b) Khi y = 8 suy ra: 2x2 = 8 ⇒ x = 2 hoặc x = -2
Do đó ta có: B1(- 2;8) và B2(2;8)
Đường thẳng y = a’x + b trải qua A và B1 nên tọa độ của A và B1 nghiệm đúng phương trình.
Điểm A: – 2 = – a’ + b’
Điểm B: 8 = – 2a’ + b’
Hai số a’ và b’ là nghiệm của hệ phương trình:

Phương trình đường thẳng AB1 là y = – 6x – 4
Đường thẳng y = a’x + b’ trải qua A và B2 nên tọa độ của A và B2 nghiệm đúng phương trình đường thẳng.
Điểm A: 2 = -a’ + b’
Điểm B2: 8 = 2a’ + b’
Hai số a’ và b’ là nghiệm của hệ phương trình

Phương trình đường thẳng AB2 là y = 2x + 4.
Tải thêm tài liệu liên quan đến nội dung bài viết Đường thẳng y = ax 2 trải qua điểm A 1 5 thi Reply
Reply
 7
7
 0
0
 Chia sẻ
Chia sẻ
Chia Sẻ Link Down Đường thẳng y = ax 2 trải qua điểm A 1 5 thi miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Đường thẳng y = ax 2 trải qua điểm A 1 5 thi tiên tiến và phát triển nhất và ShareLink Download Đường thẳng y = ax 2 trải qua điểm A 1 5 thi miễn phí.