Thủ Thuật Hướng dẫn Toán 11 bài 3 một số trong những phương trình lượng giác thường gặp Mới Nhất
Quý khách đang tìm kiếm từ khóa Toán 11 bài 3 một số trong những phương trình lượng giác thường gặp được Cập Nhật vào lúc : 2022-10-28 23:35:07 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Mục lục Giải Toán 11 Bài 3: Một số phương trình lượng giác thường gặp
Video giải Toán 11 Bài 3: Một số phương trình lượng giác thường gặp
Hoạt động 1 trang 29 SGK Toán lớp 11 Đại số: Giải những phương trình sau
a) 2sinx − 3 = 0 là phương trình số 1 riêng với sinx.
b) 3tanx+1=0 là phương trình số 1 riêng với tanx.
Lời giải:
a) 2sinx – 3 = 0
⇔sinx=32
Phương trình vô nghiệm vì sinx≤1<32 với mọi x.
b) 3tanx+1=0
⇔tanx=−33
⇔tanx=tan−π6
⇔x=−π6+kπ,k∈ℤ
Vậy những nghiệm của phương trình là x=−π6+kπ,k∈ℤ .
Hoạt động 2 trang 31 SGK Toán lớp 11 Đại số: Giải những phương trình sau:
a) 3cos2x − 5cos x + 2 = 0 ;
b) 3tan23−23tanx+3=0.
Lời giải:
a) 3cos2x – 5cosx + 2 = 0
Đặt cosx = t với Đk -1 ≤ t ≤ 1 (*), ta được phương trình bậc hai theo t:
3t2 - 5t + 2 = 0 (1)
Δ = (-5)2 - 4.3.2 = 1
Phương trình (1) có hai nghiệm là:
t1=−(−5)+12.3=66=1 (thỏa mãn nhu cầu)
t2=−(−5)−12.3=46=23 (thỏa mãn nhu cầu)
Trường hợp 1: cosx = 1
⇔x=k2π, k∈ℤ
Trường hợp 2: cosx=23⇔x=±arccos23+k2π, k∈ℤ
Vậy những nghiệm của phương trình là x=k2π;x=±arccos23+k2π, k∈ℤ.
b) 3tan2x−23tanx+3=0
Đặt tanx = t, ta được phương trình bậc hai theo t:
3t2−23t+3=0 (1)
Δ=(−23)2−4.3.3=−24<0
Vậy phương trình (1) vô nghiệm, nên không còn x thỏa mãn nhu cầu đề bài.
Hoạt động 3 trang 32 SGK Toán lớp 11 Đại số: Hãy nhắc lại:
a) Các hằng đẳng thức lượng giác cơ bản;
b) Công thức cộng;
c) Công thức nhân đôi;
d) Công thức biến hóa tích thành tổng và tổng thành tích.
Lời giải:
a) Các hằng đẳng thức lượng giác cơ bản:
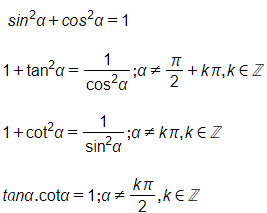
b) Công thức cộng:
cos(a - b) = cosa.cosb + sina.sinb
cos(a + b) = cosa.cosb - sina.sinb
sin(a + b) = sina.cosb + cosa.sinb
sin(a - b) = sina.cosb - cosa.sinb
tan(a−b)=tana−tanb1+tana.tanb
tan(a+b)=tana+tanb1−tana.tanb
c) Công thức nhân đôi:
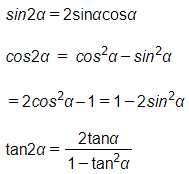
d) Công thức biến hóa tích thành tổng:
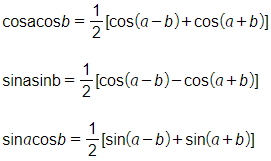
Công thức biến hóa tổng thành tích:
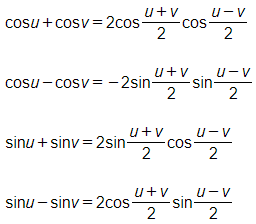
Hoạt động 4 trang 34 SGK Toán lớp 11 Đại số: Giải phương trình
3cos26x + 8sin3xcos3x – 4 = 0.
Lời giải:
3cos26x + 8sin3xcos3x – 4 = 0
⇔ 3(1 – sin26x) + 4sin 6x – 4 = 0 (vận dụng hằng đẳng thức và công thức nhân đôi)
⇔ –3sin26x + 4sin6x – 1 = 0
Đặt sin 6x = t với Đk −1≤t≤1 (*), ta được phương trình bậc hai theo t:
−3t2+4t−1=0(1)
Δ=42−4.(−1).(−3)=4
Phương trình (1) có hai nghiệm là:
t1=−4+42⋅(−3)=13(TM)
t2=−4−42⋅(−3)=1(TM)
Ta có:
Trường hợp 1:
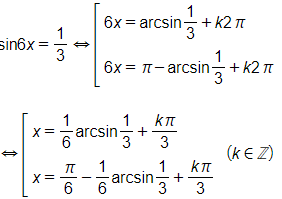
Trường hợp 2: sin6x = 1
⇔sin6x=sinπ2
⇔6x=π2+k2π
⇔x=π12+kπ3,k∈ℤ
Vậy nghiệm của phương trình là: x=π12+kπ3, x=16arcsin13+kπ3,
x=π6−16arcsin13+kπ3 k∈ℤ.
Hoạt động 5 trang 35 SGK Toán lớp 11 Đại số: Dựa vào công thức cộng đã học:
sin (a + b) = sinacosb + sinbcosa
cos (a + b) = cosacosb − sinasinb
sin (a − b) = sinacosb − sinbcosa
cos (a − b) = cosacosb + sinasinb
và kết quả cosπ4=sinπ4=22 , hãy chứng tỏ rằng:
a) sinx+cosx=2cosx−π4;
b) sinx−cosx=2sinx−π4.
Lời giải:
a) sinx+cosx=2cosx−π4
Ta có:
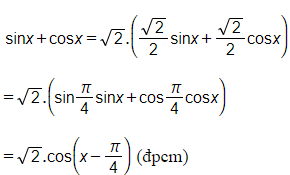
Cách khác:
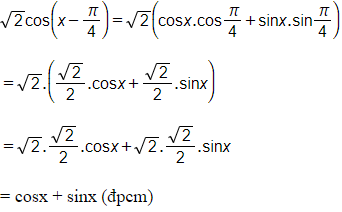
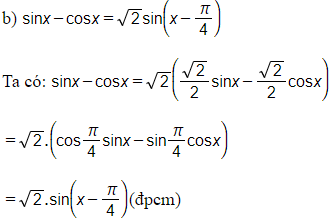
Cách khác:
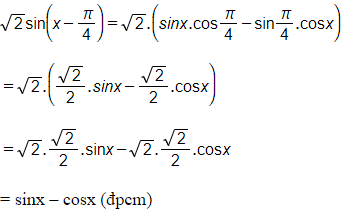
Hoạt động 6 trang 36 SGK Toán lớp 11 Đại số: Giải phương trình: 3sin3x−cos3x=2
Lời giải:
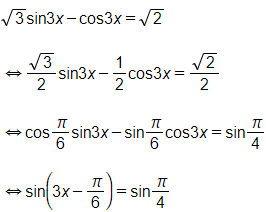
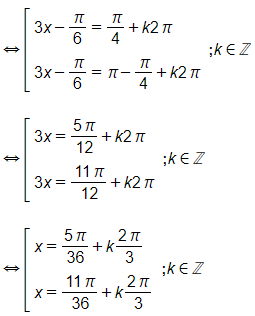
Vậy những nghiệm của phương trình là x=5π36+k2π3; x=11π36+k2π3k∈ℤ.
Bài 1 trang 36 SGK Toán lớp 11 Đại số: Giải phương trình: sin2x – sinx = 0.
Lời giải:
sin2x−sinx=0
⇔sinx(sinx−1)=0
⇔sinx=0sinx−1=0
⇔sinx=0sinx=1
⇔x=kπx=π2+k2π (k∈ℤ)
Vậy nghiệm của phương trình là x=kπ; x=π2+k2π (k∈ℤ).
Bài 2 trang 36 SGK Toán lớp 11 Đại số: Giải những phương trình sau:
a) 2cos2x – 3cosx +1 = 0;
b) 2sin2x+2sin4x=0.
Lời giải:
a) 2cos2x – 3cosx + 1 = 0
Đặt cosx=t(−1≤t≤1)
Phương trình trở thành: 2t2 – 3t +1 = 0
⇔t=1 (TM) t=12(TM)
Với t = 1 ⇒cosx=1 ⇔x=k2π,k∈ℤ
Với t=12 ⇒cosx=12 ⇔x=±π3+k2π,k∈ℤ
Vậy những nghiệm của phương trình là x=k2π; x=±π3+k2π,k∈ℤ.
b) 2sin2x+2sin4x=0
⇔2sin2x+22sin2xcos2x=0
⇔2sin2x1+2cos2x=0
⇔sin2x=01+2cos2x=0
⇔sin2x=0cos2x=−12
⇔2x=kπ2x=±3π4+k2πk∈ℤ
⇔x=kπ2x=±3π8+kπ(k∈ℤ)
Vậy nghiệm của phương trình là x=kπ2; x=±3π8+kπ (k∈ℤ).
Bài 3 trang 37 SGK Toán lớp 11 Đại số: Giải những phương trình sau:
a) sin2x2−2cosx2+2=0;
b) 8cos2x + 2sinx – 7 = 0;
c) 2tan2x + 3tanx +1 = 0;
d) tanx – 2cotx + 1 = 0.
Lời giải:
a) sin2x2−2cosx2+2=0
Ta có: sin2x2=1−cos2x2
Phương trình tương tự với:
1−cos2x2−2cosx2+2=0 (*)
⇔cos2x2+2cosx2−3=0
Đặt cosx2=t (-1≤t≤1)
Phương trình trở thành:
t2 +2t - 3 = 0
⇔t=1 (TM)t=−3 (L)
Với t = 1 ⇒cosx2=1 ⇔x2=k2π ⇔x=k4π (k∈ℤ)
Vậy nghiệm của phương trình là x=k4π (k∈ℤ).
b) 8cos2x + 2sinx – 7 = 0
Ta có: cos2x = 1 – sin2x
Phương trình tương tự với:
8(1 – sin2x) + 2sinx – 7 = 0
⇔8sin2x–2sinx–1=0
Đặt sinx = t, (−1≤t≤1)
Phương trình trở thành: 8t2 – 2t – 1 = 0
⇔t=12(TM)t=−14(TM)
Với t=12⇒sinx=12 ⇔x=π6+k2πx=5π6+k2π(k∈ℤ)
Với t=−14⇒sinx=−14 ⇔x=arcsin−14+k2πx=π−arcsin−14+k2π(k∈ℤ)
Vậy những nghiệm của phương trình là
x=π6+k2π; x=5π6+k2π; x=arcsin−14+k2π;x=π−arcsin−14+k2π(k∈ℤ)
c) 2tan2x + 3tanx +1 = 0
Điều kiện: x≠π2+kπ,k∈ℤ
Đặt tanx = t, phương trình trở thành:
2t2 + 3t +1 = 0
⇔t=−1t=−12
⇔tanx=−1tanx=−12
⇔x=−π4+kπx=arctan−12+kπ(k∈ℤ)
Vậy những nghiệm của phương trình là x=−π4+kπ; x=arctan−12+kπk∈ℤ.
d) tanx – 2cotx + 1 = 0
Điều kiện: sinx≠0cosx≠0⇔x≠kπx≠π2+kπ⇔x≠kπ2 (k∈ℤ)
Ta có: tanx – 2cotx + 1 = 0
⇔tanx−2tanx+1=0
⇒tan2x+tanx–2=0
Đặt tanx = t, phương trình trở thành:
t2 + t – 2 = 0 ⇔t=1t=−2 ⇔tanx=1tanx=−2
⇔x=π4+kπx=arctan(−2)+kπ(k∈ℤ) (Thỏa mãn)
Vậy nghiệm của phương trình là: x=π4+kπ, x=arctan(−2)+kπ,(k∈ℤ)
Bài 4 trang 37 SGK Toán lớp 11 Đại số: Giải những phương trình sau:
a) 2sin2x + sinxcosx − 3cos2 x = 0;
b) 3sin2x − 4sinxcosx + 5cos2x = 2;
c) sin2x+sin2x−2cos2x =12;
d) 2cos2x−33sin2x−4sin2x=−4.
Lời giải:
a) 2sin2x + sinxcosx − 3cos2 x = 0
Trường hợp 1: cosx=0⇔sin2x=1
Khi đó ta có 2.1 + 0 – 0 = 0 (vô lý)
Trường hợp 2: cosx≠0⇒x≠π2+kπ,(k∈ℤ)
Chia cả hai vế của phương trình cho cos2x ta được:
sin2xcos2x+sinxcosx−3=0⇔2tan2x+tanx−3=0
Đặt t = tanx, khi đó phương trình trở thành: 2t2+t−3=0⇔t=1t=−32
Với t = 1 ⇒tanx=1⇔x=π4+kπ,(k∈ℤ) (Thỏa mãn)
Với t=−32⇒tanx=−32 ⇔x=arctan−32+kπ,(k∈ℤ) (Thỏa mãn)
Vậy những nghiệm của phương trình là x=π4+kπ,(k∈ℤ); x=arctan−32+kπ,(k∈ℤ).
b) 3sin2x − 4sinxcosx + 5cos2x = 2
Trường hợp 1: cosx=0⇔sin2x=1
Khi đó ta có 3.1 + 0 – 0 = 2 (vô lý)
Trường hợp 2: cosx≠0⇒x≠π2+kπ,(k∈ℤ)
Chia cả hai vế của phương trình cho cos2x ta được:
3sin2xcos2x−4sinxcosx+5=2cos2x
⇔3tan2x−4tanx+5=2tan2x+1
⇔tan2x−4tanx+3=0
Đặt t = tanx, khi đó phương trình trở thành: t2−4t+3=0⇔t=1t=3
Với t = 1 ⇒tanx=1 ⇔x=π4+kπ,(k∈ℤ) (tm)
Với t = 3 ⇒tanx=3 ⇔x=arctan3+kπ,(k∈ℤ) (tm)
Vậy những nghiệm của phương trình là x=π4+kπ,(k∈ℤ); x=arctan3+kπ,(k∈ℤ).
c) sin2x+sin2x−2cos2x =12
⇔sin2x+2sinxcosx−2cos2x=12
⇔2sin2x+4sinxcosx−4cos2x=1
Trường hợp 1: cosx=0⇔sin2x=1
Khi đó ta có: 2 + 0 – 0 = 1 (vô nghiệm)
Trường hợp 2: cosx≠0⇒x≠π2+kπ,(k∈ℤ)
Chia cả hai vế của phương trình cho cos2x ta được:
2sin2xcos2x+4sinxcosx−4=1cos2x
⇔2tan2x+4tanx−4=tan2x+1
⇔tan2x+4tanx−5=0
Đặt t = tanx, khi đó phương trình trở thành: t2+4t−5=0⇔t=1t=−5
Với t = 1
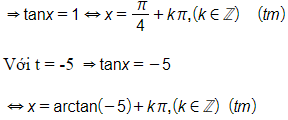
Vậy những nghiệm của phương trình là x=π4+kπ,(k∈ℤ); x=arctan(−5)+kπ,(k∈ℤ)
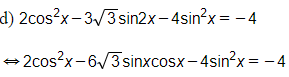
Trường hợp 1: cosx=0⇔sin2x=1
Khi đó ta 0 + 0 - 4 = - 4 (Luôn đúng)
⇒x=π2+kπ,(k∈ℤ) là nghiệm của phương trình.
Trường hợp 2: cosx≠0⇒x≠π2+kπ,(k∈ℤ)
Chia cả hai vế của phương trình cho ta được:
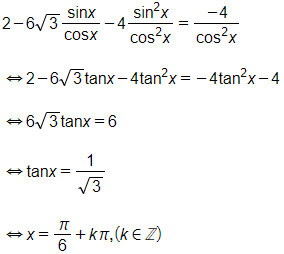
Vậy những nghiệm của phương trình là x=π2+kπ,(k∈ℤ); x=π6+kπ,(k∈ℤ).
Bài 5 trang 37 SGK Toán lớp 11 Đại số: Giải những phương trình sau:
a) cosx−3sin2x=2;
b) 3sin3x − 4cos3x = 5 ;
c) 2sinx+2cosx−2=0;
d) 5cos2x + 12sin2x − 13 = 0.
Lời giải:
a) cosx−3sin2x=2
⇔12cosx−32sinx=22
⇔cosxcosπ3−sinxsinπ3=22
⇔cosx+π3=cosπ4
⇔x+π3=π4+k2πx+π3=−π4+k2π k∈ℤ
⇔x=−π12+k2πx=−7π12+k2π(k∈ℤ)
Vậy nghiệm của phương trình là x=−π12+k2π; x=−7π12+k2π(k∈ℤ)
b) 3sin3x − 4cos3x = 5
⇔35sin3x−45cos3x=1
Đặt sinα=35cosα=45 , phương trình trở thành:
sin3xsinα–cos3xcosα = 1
⇔cos3xcosα−sin3xsinα=−1
⇔cos(3x+α)=–1
⇔3x+α=π+k2π
⇔3x=π−α+k2π
⇔x=π−α3+k2π3 (k∈ℤ)
Vậy những nghiệm của phương trình là x=π−α3+k2π3 (k∈ℤ) với ( sinα=35,cosα=45).
c) 2sinx+2cosx−2=0
⇔2sinx+2cosx=2
⇔222sinx+222cosx=222
⇔12sinx+12cosx=12
⇔sinxsinπ4+cosxcosπ4=12
⇔cosx−π4=cosπ3
⇔x−π4=π3+k2πx−π4=−π3+k2π k∈ℤ
⇔x=7π12+k2πx=−π12+k2π(k∈ℤ)
Vậy những nghiệm của phương trình là x=7π12+k2π hoặc x=−π12+k2π, k∈ℤ.
d) 5cos2x + 12sin2x − 13 = 0
⇔513cos2x+1213sin2x=1
Đặt sinα=1213cosα=513, khi đó phương trình trở thành:
cos2xcosα+sin2xsinα=1
⇔cos2x–α=1
⇔2x−α=k2π
⇔x=α2+kπ (k∈ℤ)
Vậy nghiệm của phương trình là x=α2+kπ,(k∈ℤ) với sinα=1213;cosα=513.
Bài 6 trang 37 SGK Toán lớp 11 Đại số: Giải những phương trình sau:
a) tan(2x + 1)tan(3x – 1) = 1;
b) tanx+tanx+π4=1.
Lời giải:
a) tan(2x + 1)tan(3x – 1) = 1
Điều kiện: cos(2x+1)≠0cos(3x−1)≠0
⇔2x+1≠π2+kπ3x−1≠π2+kπ
⇔2x≠π2−1+kπ3x≠π2+1+kπ
⇔x≠π4−12+kπ2x≠π6+13+kπ3 k∈ℤ
Ta có: tan(2x + 1)tan(3x – 1) = 1
⇔tan(2x+1)=1tan(3x−1)
⇔tan(2x+1)=cot(3x−1)
⇔tan(2x+1)=tanπ2−3x+1
⇔2x+1=π2−3x+1+kπ
⇔5x=π2+kπ
⇔x=π10+kπ5,(k∈ℤ)(tm)
Vậy những nghiệm của phương trình là x=π10+kπ5 (k∈ℤ).
b) tanx+tanx+π4=1
Điều kiện: cosx≠0cosx+π4≠0 ⇔x≠π2+kπx+π4≠π2+kπ ⇔x≠π2+kπx≠π4+kπk∈ℤ
Ta có: tanx+tanx+π4=1
⇔tanx+tanx+tanπ41−tanxtanπ4=1
⇔tanx+tanx+11−tanx=1
⇔tanx–tan2x+tanx+1=1−tanx
⇔tan2x−3tanx=0
⇔tanxtanx–3=0
⇔tanx=0tanx=3
⇔x=kπx=arctan3+kπ(k∈ℤ) (Thỏa mãn)
Vậy nghiệm của phương trình là x=kπ; x=arctan3+kπ,(k∈ℤ)
Bài giảng Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (Tiết 1)
Bài giảng Toán 11 Bài 3: Một số phương trình lượng giác thường gặp (Tiết 2)
Xem thêm lời giải bài tập Toán lớp 11 Đại số và Giải tích hay, rõ ràng khác:
Ôn tập chương 1
Bài 1: Quy tắc đếm
Bài 2: Hoán vị - chỉnh hợp – tổng hợp
Bài 3: Nhị thức Niu-tơn
Bài 4: Phép thử và biến cố
Xem thêm tài liệu Toán lớp 11 Đại số và Giải tích hay, rõ ràng khác:
Lý thuyết Một số phương trình lượng giác thường gặp.
Trắc nghiệm Một số phương trình lượng giác thường gặp có đáp án
Tải thêm tài liệu liên quan đến nội dung bài viết Toán 11 bài 3 một số trong những phương trình lượng giác thường gặp Học Tốt Phương trình Reply
Reply
 6
6
 0
0
 Chia sẻ
Chia sẻ
Share Link Down Toán 11 bài 3 một số trong những phương trình lượng giác thường gặp miễn phí
Bạn vừa Read Post Với Một số hướng dẫn một cách rõ ràng hơn về Clip Toán 11 bài 3 một số trong những phương trình lượng giác thường gặp tiên tiến và phát triển nhất và Chia SẻLink Download Toán 11 bài 3 một số trong những phương trình lượng giác thường gặp Free.