Mẹo về Cho đa giác lồi n đỉnh số tam giác có 3 đỉnh 2022
Quý khách đang tìm kiếm từ khóa Cho đa giác lồi n đỉnh số tam giác có 3 đỉnh được Cập Nhật vào lúc : 2022-07-17 06:15:06 . Với phương châm chia sẻ Mẹo về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc tài liệu vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Đáp án B
Nội dung chính- CÂU HỎI HOT CÙNG CHỦ ĐỀ
- B. 4057.
- Chọn B. Mỗi cách chọn ngẫu nhiên 3 đỉnh từ những đỉnh của đa giác sẽ tạo ra một tam giác và số tam giác là nΩ=C203. Gọi là biến cố 3 đỉnh được chọn tạo thành một tam giác không còn cạnh nào là cạnh của đa giác đã cho. Ta có mỗi tam giác thuộc Ω thì có một trong 4 trường hợp sau: TH1: Cả 3 cạnh của tam giác là những cạnh của đa giác, trường hợp này sẽ không còn còn tam giác nào. TH2: Chỉ có 2 cạnh của tam giác là cạnh của đa giác, khi đó đỉnh chung của 2 cạnh này sẽ là đỉnh của đa giác ban đầu, trường hợp này còn có 20 tam giác. TH3: Chỉ có một cạnh của tam giác là cạnh của đa giác khi đó ứng với mỗi cạnh bất ký của đa giác thì sẽ có được 16 tam giác thỏa mãn nhu cầu, vậy trường hợp này sẽ có được 20x16 = 320 tam giác. TH4: Không có cạnh nào của tam giác là cạnh của đa giác, khi đó toàn bộ những cạnh của tam giác đều là những đường chéo của đa giác. Từ đây ta có nA=nΩ−20−320=800 tam giác. Vậy xác suất để chọn được 3 đỉnh tạo thành tam giác không còn cạnh nào của đa giác đã cho là PA=nAnΩ=4057.
- CÂU HỎI HOT CÙNG CHỦ ĐỀ
Phương pháp giải:
- Tính số thành phần của không khí mẫu.
- Gọi A là biến cố: “3 đỉnh được chọn tạo thành 1 tam giác không còn cạnh nào là cạnh của đa giác đã cho”, suy ra biến cố đối A¯: “3 đỉnh được chọn tạo thành 1 tam giác có cạnh là cạnh của đa giác đã cho”.
- Tính số thành phần của biến cố đối, xét 2 TH:
+ TH1: Số tam giác chỉ chứa 2 cạnh của đa giác.
+ TH2: Số tam giác chứa đúng 1 cạnh của đa giác.
- Sử dụng công thức tính xác suất PA=1-PA¯=1-nA¯nΩ.
Giải rõ ràng:
ngẫu nhiên 3 đỉnh của đa giác, suy ra số thành phần của không khí mẫu là C203=1140
Gọi A là biến cố: “3 đỉnh được chọn tạo thành 1 tam giác không còn cạnh nào là cạnh của đa giác đã cho”.
⇒A¯: “3 đỉnh được chọn tạo thành 1 tam giác có cạnh là cạnh của đa giác đã cho”.
TH1: Số tam giác chỉ chứa 2 cạnh của đa giác là số tam giác có 3 đỉnh liên tục của đa giác thì có 20 tam giác như vậy.
TH2: Số tam giác chứa đúng 1 cạnh của đa giác là số tam giác có 2 đỉnh là 2 đỉnh liên tục của đa giác và đỉnh còn sót lại không tiếp theo đó hai đỉnh kia.
Xét 1 cạnh bất kì, ta có C161 cách chọn một đỉnh trong 16 đỉnh còn sót lại (trừ 2 đỉnh đã chọn và 2 đỉnh kề với nó).
⇒ Có 20.16=320 tam giác.
⇒nA¯=20+320=340
Vậy xác suất của biến cố A là PA=1-PA¯=1-3401140=4057
Câu hỏi trên thuộc đề trắc nghiệm dưới đây !
Số vướng mắc: 1538
Chọn D
Lời giải. Số tam giác tạo thành có 3 đỉnh là 3 đỉnh của đa giác là Cn3
Số tam giác tạo thành có đúng 2 cạnh là cạnh của đa giác là n
Số tam giác tạo thành có đúng 1 cạnh là cạnh của đa giác là n(n-4)
(Đk n∈ℕ và n<4 )
→số tam giác tạo thành không còn cạnh nào là cạnh của đa giác là
Theo giả thiết, ta có
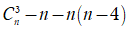
⇔n=35(thỏa mãn)n=4(loại)
CÂU HỎI HOT CÙNG CHỦ ĐỀ
15/09/2022 707
B. 4057.
Đáp án đúng chuẩn
Chọn B. Mỗi cách chọn ngẫu nhiên 3 đỉnh từ những đỉnh của đa giác sẽ tạo ra một tam giác và số tam giác là nΩ=C203. Gọi là biến cố 3 đỉnh được chọn tạo thành một tam giác không còn cạnh nào là cạnh của đa giác đã cho. Ta có mỗi tam giác thuộc Ω thì có một trong 4 trường hợp sau: TH1: Cả 3 cạnh của tam giác là những cạnh của đa giác, trường hợp này sẽ không còn còn tam giác nào. TH2: Chỉ có 2 cạnh của tam giác là cạnh của đa giác, khi đó đỉnh chung của 2 cạnh này sẽ là đỉnh của đa giác ban đầu, trường hợp này còn có 20 tam giác. TH3: Chỉ có một cạnh của tam giác là cạnh của đa giác khi đó ứng với mỗi cạnh bất ký của đa giác thì sẽ có được 16 tam giác thỏa mãn nhu cầu, vậy trường hợp này sẽ có được 20x16 = 320 tam giác. TH4: Không có cạnh nào của tam giác là cạnh của đa giác, khi đó toàn bộ những cạnh của tam giác đều là những đường chéo của đa giác. Từ đây ta có nA=nΩ−20−320=800 tam giác. Vậy xác suất để chọn được 3 đỉnh tạo thành tam giác không còn cạnh nào của đa giác đã cho là PA=nAnΩ=4057.
CÂU HỎI HOT CÙNG CHỦ ĐỀ
Một cơ sở sản xuất có hai bể nước hình trụ có độ cao bằng nhau, bán kính đáy lần lượt bằng 1m và 1,2m Chủ cơ sở dự tính làm một bể nước mới, hình trụ, có cùng độ cao và hoàn toàn có thể tích bằng tổng thế tích của hai bể nước trên. Bán kính đáy của bể nước dự tính làm sớm nhất với kết quả nào dưới đây?
Xem đáp án » 15/09/2022 4,435
Thể tích khối cầu có bán kính r là:
Xem đáp án » 14/09/2022 1,552
Cho hàm số y = f(x) có đạo hàm liên tục trên R Biết hàm số y = f’(x) có đồ thị như hình vẽ. Gọi S là tập hợp những giá trị nguyên để hàm số gx=fx+m nghịch biến trên khoảng chừng (1;2) Hỏi S có bao nhiêu thành phần?
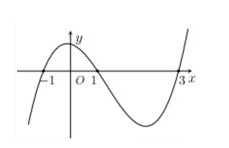
Xem đáp án » 15/09/2022 1,146
Có bao nhiêu giá trị nguyên của tham số m trong [-2020;2020] để phương trình logmx=2logx+1 có nghiệm duy nhất?
Xem đáp án » 15/09/2022 1,067
Tìm toàn bộ những giá trị của tham số m để đồ thị hàm số y=2x−4x−m có quán cận đứng
Xem đáp án » 14/09/2022 954
Cho hình lập phương ABCD.A’B’C’D’ có tâm O Gọi I là tâm của hình vuông vắn A’B’C’D’ và M là yếu tố thuộc đoạn thẳng OI sao cho MO=2MI Khi đó côsin góc tạo bởi hai mặt phẳng (MC'D’) và (MAB) bằng
Xem đáp án » 15/09/2022 953
Cho hình chóp S.ABCD có đáy ABCD là hình vuông vắn cạnh a,SD=3a2, hình chiếu vuông góc của S trên mặt phẳng (ABCD) là trung điểm của cạnh AB Tính theo a thể tích khối chóp S.ABCD
Xem đáp án » 14/09/2022 899
Tìm tập hợp toàn bộ những giá trị của tham số m để hàm số y=1log3x2−2x+3m có tập xác lập là R
Xem đáp án » 14/09/2022 844
Có bao nhiêu cách sắp xếp 8 học viên thành một hàng dọc?
Xem đáp án » 14/09/2022 663
Giới hạn lim2n2−1 bằng
Xem đáp án » 14/09/2022 662
Cho hình chóp S.BCD có đáy ABCD hình vuông vắn cạnh a Tam giác SAB đều và nằm trong mặt phẳng vuông góc với đáy, bán kính mặt cầu ngoại tiếp hình chóp là:
Xem đáp án » 15/09/2022 636
Cho hàm số y =f(x) có bảng biến thiên như hình dưới đây. Tìm giá trị lớn số 1 của hàm số gx=f4x−x2+13x3−3x2+8x−53 trên đoạn [1;3]
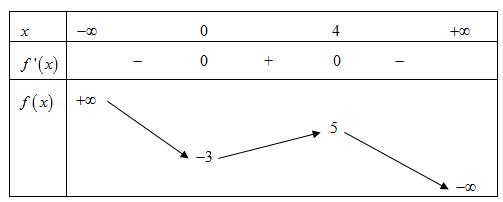
Xem đáp án » 15/09/2022 611
Cho mặt cầu S(O;r), mặt phẳng (P) cách tâm O một khoảng chừng bằng r2 cắt mặt cầu (S) theo giao tuyến là một đường tròn. Hãy tính theo r chu vi của đường tròn là giao tuyến của mặt phẳng (P) và mặt cầu (S)
Xem đáp án » 14/09/2022 583
Cho số tự nhiên n thỏa mãn nhu cầu Cn0+Cn1+Cn2=11. Số hạng chứa x7 trong khai triển x3−1x2n bằng
Xem đáp án » 14/09/2022 536
Đường cong trong hình bên là đồ thị của hàm số nào trong bốn hàm số dưới đây?
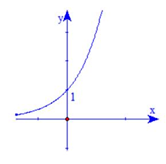
Xem đáp án » 14/09/2022 446
 Reply
Reply
 2
2
 0
0
 Chia sẻ
Chia sẻ
Share Link Down Cho đa giác lồi n đỉnh số tam giác có 3 đỉnh miễn phí
Bạn vừa tìm hiểu thêm nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Video Cho đa giác lồi n đỉnh số tam giác có 3 đỉnh tiên tiến và phát triển nhất và Chia Sẻ Link Down Cho đa giác lồi n đỉnh số tam giác có 3 đỉnh miễn phí.