Kinh Nghiệm về Áp dụng tỉ số lượng giác nào của góc n để tính nk nhanh nhất có thể 2022
Quý khách đang tìm kiếm từ khóa Áp dụng tỉ số lượng giác nào của góc n để tính nk nhanh nhất có thể được Update vào lúc : 2022-07-15 12:45:06 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.day kem Công thức lượng giác là một phần trong toán học, nó cực kỳ quan trọng trong việc học toán, nhưng khổ nỗi cũng rất dể quên, thật nhiều người đang tìm ra cách học nhanh những công thức lượng giác để hoàn toàn có thể nhớ lâu hơn, ngày hôm nay gia su Trí Tuệ Việt xin chia sẽ cho những bạn những thủ thuật và mẹo để học những công thức lượng giác thuộc và khắc ghi trong đầu một cách nhanh gọn, toàn bộ chúng ta khởi đầu nhé
Nội dung chính- Video học công thức lượng giác
- Học công thức lượng giác bằng thơ
- Học công thức lượng giác “thần chú”
- CÔNG THỨC TÍNH NGUYÊN HÀM
- Tất cả những công thức hóa học lớp 8
- công thức đạo hàm

Video học công thức lượng giác
Học công thức lượng giác bằng thơ
CÔNG THỨC + TRONG LƯƠNG GIÁC Cos + cos = 2 cos cos cos trừ cos = trừ 2 sin sin Sin + sin = 2 sin cos sin trừ sin = 2 cos sin. Sin thì sin cos cos sin Cos thì cos cos sin sin “coi chừng” (dấu trừ). Tang tổng thì lấy tổng tang
Chia một trừ với tích tang, dễ òm.
HÀM SỐ LƯỢNG GIÁC
Bắt được quả tang Sin nằm trên cos ([email protected] = [email protected]:[email protected]) Cotang dại dột Bị cos đè cho. ([email protected] = [email protected]:[email protected]) Version 2: Bắt được quả tang Sin nằm trên cos Côtang cãi lại
Cos nằm trên sin!
GIÁ TRỊ LƯỢNG GIÁC CỦA CÁC CUNG ĐẶC BIỆT
Cos đối, sin bù, phụ chéo, khác pi tan
Cosin của 2 góc đối bằng nhau; sin của 2 góc bù nhau thì bằng nhau; phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tan góc này = cot góc kia; tan của 2 góc hơn kém pi thì bằng nhau.
CÔNG THỨC LƯỢNG GIÁC NHÂN BA
Nhân ba một góc bất kỳ, sin thì ba bốn, cos thì bốn ba, dấu trừ đặt giữa 2 ta, lập phương chỗ bốn,
… thế là ok.
6.Công thức gấp hai: +Sin gấp hai = 2 sin cos +Cos gấp hai = bình cos trừ bình sin = trừ 1 + 2 lần bình cos = + 1 trừ 2 lần bình sin +Tang gấp hai Tang đôi ta lấy đôi tang (2 tang)
Chia 1 trừ lại bình tang, ra liền.
Cách nhớ công thức: tan(a+b)=(tan+tanb)/1-tana.tanb là tan một tổng 2 tầng lầu rộng trên thượng tầng tan + tan tan dưới hạ tầng số 1 ngang tàng
dám trừ một tích tan tan oai hùng
CÔNG THỨC LƯỢNG GIÁC BIẾN ĐỔI TÍCH THÀNH TỔNG Cos cos nửa cos-+, + cos-trừ Sin sin nửa cos-trừ trừ cos-+
Sin cos nửa sin-+ + sin-trừ
CÔNG THỨC LƯỢNG GIÁC BIẾN ĐỔI TỔNG THÀNH TÍCH sin tổng lập tổng sin cô cô tổng lập hiệu đôi cô đôi chàng còn tan tử + đôi tan (hoặc là: tan tổng lập tổng 2 tan) một trừ tan tích mẫu mang thương sầu gặp hiệu ta chớ lo âu,
đổi trừ thành + ghi sâu vào lòng
Một phiên bản khác của câu Tan mình + với tan ta, bằng sin 2 đứa trên cos ta cos mình… là
tanx + tany: tình mình + lại tình ta, sinh ra 2 người con mình con ta
tanx – tan y: tình mình hiệu với tình ta sinh ra hiệu chúng, con ta con mình
CÔNG THỨC CHIA ĐÔI (tính theo t=tg(a/2)) Sin, cos mẫu giống nhau chả khác Ai cũng là một + bình tê (1+t^2) Sin thì tử có 2 tê (2t),
cos thì tử có một trừ bình tê (1-t^2).
HỆ THỨC LƯỢNG TRONG TAM GIÁC VUÔNG
Sao Đi Học ( Sin = Đối / Huyền) Cứ Khóc Hoài ( Cos = Kề / Huyền) Thôi Đừng Khóc ( Tan = Đối / Kề)
Có Kẹo Đây ( Cotan = Kề/ Đối)
Sin : đi học (cạnh đối – cạnh huyền) Cos: không hư (cạnh đối – cạnh huyền) Tang: đoàn kết (cạnh đối – cạnh kề)
Cotang: kết đoàn (cạnh kề – cạnh đối)
Tìm sin lấy đối chia huyền Cosin lấy cạnh kề, huyền chia nhau Còn tang ta hãy tính sau Đối trên, kề dưới chia nhau ra liền Cotang cũng dễ ăn tiền
Kề trên, đối dưới chia liền là ra
Sin bù, cos đối, hơn kém pi tang, phụ chéo. +Sin bù :Sin(180-a)=sina +Cos đối :Cos(-a)=cosa +Hơn kém pi tang : Tg(a+180)=tga Cotg(a+180)=cotga
+Phụ chéo là 2 góc phụ nhau thì sin góc này = cos góc kia, tg góc này = cotg góc kia.
Công thức tổng quát hơn về việc hơn kém pi như sau: Hơn kém bội 2 pi sin, cos Tang, cotang hơn kém bội pi. Sin(a+k.2.180)=sina ; Cos(a+k.2.180)=cosa Tg(a+k180)=tga ; Cotg(a+k180)=cotga *sin bình + cos bình = 1 *Sin bình = tg bình trên tg bình + 1. *cos bình = 1 trên 1 + tg bình. *Một trên cos bình = 1 + tg bình. *Một trên sin bình = 1 + cotg bình.
(Chú ý sin *; cos @ ; tg @ ;cotg * với những dấu * và @ là chúng có liên quan nhau trong CT trên
Học công thức lượng giác “thần chú”
• Sin= đối/ huyền
Cos= kề/ huyền
Tan= đối/ kề
Cot= kề/ huyền
♥Thần chú: Sin đi học, Cos không hư, tan đoàn kết, cotan kết đoàn
Hoặc: Sao đi học, cứ khóc hoài, thôi đừng khóc, có kẹo đây!
• Công thức cộng:
Cos(x y)= cosxcosy sinxsiny
Sin(x y)= sinxcosy cosxsiny
♥Thần chú: Cos thì cos cos sin sin
Sin thì sin cos cos sin rõ ràng
Cos thì đổi dấu hỡi nàng
Sin thì giữ dấu xin chàng nhớ cho!
Tan(x+y)=
Thần chú: Tan một tổng hai tầng lầu rộng
Trên thượng tầng tan cộng cùng tan
Hạ tầng số 1 ngang tàng
Dám trừ đi cả tan tan oai hùng
Hoặc: Tang tổng thì lấy tổng tang
Chia một trừ với tích tang, dễ òm.
• Công thức biến hóa tổng thành tích:
Ví dụ: cosx+cosy= 2cos cos
(Tương tự những công thức như vậy)
♥ Thần chú: cos cộng cos bằng 2 cos cos
Cos trừ cos bằng – 2 sin sin
Sin cộng sin bằng 2 sin sin
Sin trừ sin bằng 2 cos sin.
* Tan ta cộng với tan mình bằng sin hai đứa trên cos mình cos ta.
Công thức biến hóa tích thành tổng:
Ví dụ: cosxcosy=1/2[cos(x+y)+cos(x-y)] (Tương tự những công thức như vậy)
Thần chú: Cos cos nửa cos-cộng, cộng cos-trừ
Sin sin nửa cos-trừ trừ cos-cộng
Sin cos nửa sin-cộng cộng sin-trừ.
• Công thức nhân đôi:
Ví dụ: sin2x= 2sinxcosx (Tương tự những công thức như vậy)
Thần chú: Sin gấp hai = 2 sin cos
Cos gấp hai = bình cos trừ bình sin
= trừ 1 cộng hai bình cos
= cộng 1 trừ hai bình sin
(Chúng tôi chỉ việc nhớ công thức nhân đôi của cos bằng thần chú trên rồi từ đó hoàn toàn có thể suy ra công thức hạ bậc.)
Tang gấp hai=Tang đôi ta lấy đôi tang (2 tang)
Chia 1 trừ lại bình tang, ra liền.
• Hàm số lượng giác và những cung có liên quan đặc biệt quan trọng:
Ví dụ: Cos(-x)= cosx
Tan( + x)= tan x
Thần chú: Sin bù, Cos đối,Tang Pi,
Phụ nhau Sin Cos, ắt thì phân loại
Hoặc : Cos đối, sin bù, phụ chéo, hơn kém pi tang .
Thế là xong
Nguồn: Day Kem Trí Tuệ Việt sưu tầm và chia sẽ.
Trung tam gia su Trí Tuệ Việt chúc những bạn thành công xuất sắc.
BÀI VIẾT LIÊN QUAN NHẤT
CÔNG THỨC TÍNH NGUYÊN HÀM
Tất cả những công thức hóa học lớp 8
công thức đạo hàm
1. Các kiến thức và kỹ năng cần nhớ
Tỉ số lượng giác của góc nhọn
Các tỉ số lượng giác của góc nhọn (alpha ) (hình vẽ) được định nghĩa như sau:
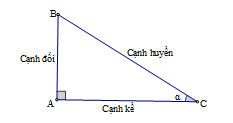
(sin alpha = dfracABBC;cos alpha = dfracACBC;)
(tan alpha = dfracABAC;cot alpha = dfracACAB).
Tính chất 1:
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
Tức là: Cho hai góc (alpha ,beta ) có (alpha + beta = 90^0)
Khi đó:
(sin alpha = cos beta ;cos alpha = sin beta ;) (tan alpha = cot beta ;cot alpha = tan beta ).
Tính chất 2:
+ Nếu hai góc nhọn (alpha ) và (beta ) có (sin alpha = sin beta ) hoặc (cos alpha = cos beta ) thì (alpha = beta )
Tính chất 3:
+ Nếu (alpha ) là một góc nhọn bất kỳ thì
(0 < sin alpha < 1;0 < cos alpha < 1,) (tan alpha > 0;cot alpha > 0)
(sin ^2alpha + cos ^2alpha = 1;) (tan alpha .cot alpha = 1)
$tan alpha = dfracsin alpha cos alpha ;cot alpha = dfraccos alpha sin alpha ;$
$1 + tan ^2alpha = dfrac1cos ^2alpha ;1 + cot ^2alpha = dfrac1sin ^2alpha $
Bảng tỉ số lượng giác những góc đặc biệt quan trọng
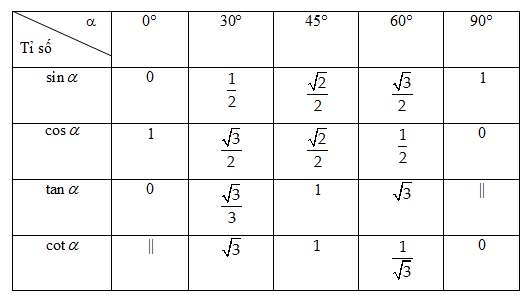
2. Các dạng toán thường gặp
Dạng 1: Tính tỉ số lượng giác của góc nhọn, tính cạnh, tính góc
Phương pháp:
Sử dụng những tỉ số lượng giác của góc nhọn, định lý Py-ta-go, hệ thức lượng trong tam giác vuông để tính toán những yếu tố thiết yếu.
Dạng 2: So sánh những tỉ số lượng giác Một trong những góc
Phương pháp:
Bước 1 : Đưa những tỉ số lượng giác về cùng loại (sử dụng tính chất "Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia")
Bước 2: Với góc nhọn (alpha ,,beta ) ta có: $sin alpha < sin beta Leftrightarrow alpha < beta ;$$cos alpha < cos beta Leftrightarrow alpha > beta ;$
$tan alpha < tan beta Leftrightarrow alpha < beta ;$$cot alpha < cot beta Leftrightarrow alpha > beta $.
Dạng 3: Rút gọn, tính giá trị biểu thức lượng giác
Phương pháp:
Ta thường sử dụng những kiến thức và kỹ năng
+ Nếu (alpha ) là một góc nhọn bất kỳ thì
(0 < sin alpha < 1;0 < cos alpha < 1), (tan alpha > 0;cot alpha > 0) , (sin ^2alpha + cos ^2alpha = 1;tan alpha .cot alpha = 1)
$tan alpha = dfracsin alpha cos alpha ;cot alpha = dfraccos alpha sin alpha ;$
$1 + tan ^2alpha = dfrac1cos ^2alpha ;1 + cot ^2alpha = dfrac1sin ^2alpha $
+ Nếu hai góc phụ nhau thì sin góc này bằng côsin góc kia, tang góc này bằng côtang góc kia.
 Reply
Reply
 9
9
 0
0
 Chia sẻ
Chia sẻ
Chia Sẻ Link Tải Áp dụng tỉ số lượng giác nào của góc n để tính nk nhanh nhất có thể miễn phí
Bạn vừa đọc Post Với Một số hướng dẫn một cách rõ ràng hơn về Review Áp dụng tỉ số lượng giác nào của góc n để tính nk nhanh nhất có thể tiên tiến và phát triển nhất và Chia Sẻ Link Down Áp dụng tỉ số lượng giác nào của góc n để tính nk nhanh nhất có thể Free.