Thủ Thuật Hướng dẫn Giải toán lớp 8 trang 40 Mới Nhất
Bạn đang tìm kiếm từ khóa Giải toán lớp 8 trang 40 được Update vào lúc : 2022-05-11 21:54:10 . Với phương châm chia sẻ Bí kíp Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.Bài 8. Cho a < b, chứng tỏ. Bài 8 trang 40 sgk toán 8 tập 2 - Liên hệ giữa thứ tự và phép nhân
Bài 8. Cho a < b, chứng tỏ:
a) 2a – 3 < 2b – 3; b) 2a – 3 < 2b + 5.
Hướng dẫn giải:
a) Ta có: a < b
=> 2a < 2b vì 2 > 0
Quảng cáo=> 2a – 3 < 2b – 3 (cộng vào cả hai vế -3)
b) Ta có: -3 < 5
=> 2b – 3 < 2b + 5 (cộng vào hai vế với 2b) mà 2a – 3 < 2b – 3 (chứng tỏ trên)
Vậy: 2a – 3 < 3b + 5 (tính chất bắc cầu)
- Giải bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34...
- Giải bài 45, 46, 47, 48, 49 trang 31, 32 sgk toán...
- Giải bài 41, 42, 43, 44 trang 31 sgk toán 8 tập 2
- Giải bài 37, 38, 39, 40 trang 30, 31 sgk toán 8...
- Giải bài 34, 35, 36 trang 25, 26 sgk toán 8 tập 2
- Giải bài 27, 28, 29, 30, 31, 32, 33 trang 22, 23...
- Giải bài 21, 22, 23, 24, 25, 26 trang 17 sgk toán...
- Giải bài 16, 17, 18, 19, 20 trang 13, 14 sgk toán...
- Giải bài 10, 11, 12, 13, 14, 15 trang 12, 13 sgk...
- Giải bài 6, 7, 8, 9 trang 9, 10 sgk toán 8 tập 2
- Giải bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34...
- Giải bài 45, 46, 47, 48, 49 trang 31, 32 sgk toán...
- Giải bài 41, 42, 43, 44 trang 31 sgk toán 8 tập 2
- Giải bài 37, 38, 39, 40 trang 30, 31 sgk toán 8...
- Giải bài 34, 35, 36 trang 25, 26 sgk toán 8 tập 2
- Giải bài 27, 28, 29, 30, 31, 32, 33 trang 22, 23...
- Giải bài 21, 22, 23, 24, 25, 26 trang 17 sgk toán...
- Giải bài 16, 17, 18, 19, 20 trang 13, 14 sgk toán...
- Giải bài 10, 11, 12, 13, 14, 15 trang 12, 13 sgk...
- Giải bài 6, 7, 8, 9 trang 9, 10 sgk toán 8 tập 2
- Giải bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34...
- Giải bài 45, 46, 47, 48, 49 trang 31, 32 sgk toán...
- Giải bài 41, 42, 43, 44 trang 31 sgk toán 8 tập 2
- Giải bài 37, 38, 39, 40 trang 30, 31 sgk toán 8...
- Giải bài 34, 35, 36 trang 25, 26 sgk toán 8 tập 2
- Giải bài 27, 28, 29, 30, 31, 32, 33 trang 22, 23...
- Giải bài 21, 22, 23, 24, 25, 26 trang 17 sgk toán...
- Giải bài 16, 17, 18, 19, 20 trang 13, 14 sgk toán...
- Giải bài 10, 11, 12, 13, 14, 15 trang 12, 13 sgk...
- Giải bài 6, 7, 8, 9 trang 9, 10 sgk toán 8 tập 2
- Giải bài 50, 51, 52, 53, 54, 55, 56 trang 33, 34...
- Giải bài 45, 46, 47, 48, 49 trang 31, 32 sgk toán...
- Giải bài 41, 42, 43, 44 trang 31 sgk toán 8 tập 2
- Giải bài 37, 38, 39, 40 trang 30, 31 sgk toán 8...
- Giải bài 34, 35, 36 trang 25, 26 sgk toán 8 tập 2
- Giải bài 27, 28, 29, 30, 31, 32, 33 trang 22, 23...
- Giải bài 21, 22, 23, 24, 25, 26 trang 17 sgk toán...
- Giải bài 16, 17, 18, 19, 20 trang 13, 14 sgk toán...
- Giải bài 10, 11, 12, 13, 14, 15 trang 12, 13 sgk...
- Giải bài 6, 7, 8, 9 trang 9, 10 sgk toán 8 tập 2
Bài 29 trang 48 sgk toán 8 tập 2
a)Giá trị của biểu thức 2x – 5 không âm;
b)Giá trị của biểu thức -3x không to nhiều hơn giá trị của biểu thức -7x + 5.
Hướng dẫn làm bài:
a)Ta có bất phương trình: 2x – 5 ≥ 0 ⇔ 2x > 5
⇔(x ge 5 over 2)
Vậy khiến cho 2x – 5 không âm thì (x ge 5 over 2) .
b)Tìm x sao cho giá trị của biểu thức -3x không to nhiều hơn giá trị của biểu thức -7x + 5.
Ta có : -3x ≤ -7x + 5 ⇔-3x + 7x ≤ 5
⇔2x ≤ 5
⇔x ≤(5 over 2)
Vậy khiến cho giá trị của -3x không to nhiều hơn giá trị của -7x + 5 thì (x le 5 over 2) .
Bài 30 trang 48 sgk toán 8 tập 2
Một người dân có số tiền không thật 70 000 đồng gồm 15 tờ giấy bạc với hai loại mệnh giá: loại 2000 đồng và loại 5000 đồng. Hỏi người đó có bao nhiêu tờ giấy bạc loại 5000 đồng?
Hướng dẫn làm bài:
Gọi x là số tờ giấy bạc loại 5000 đồng.
Số tờ giấy bạc loại 2000 đồng là 15 – x (với 0
Vì số tiền không thật 70000 nên
5000x + 2000(15 – x ) ≤ 70000
5000x + 30000 – 2000x ≤ 70000
3000x ≤ 40000
x ≤(40 over 3)
So với Đk thì (0 < x le 40 over 3) mà x là số nguyên dương nên x hoàn toàn có thể là số nguyên dương từ là 1 đến 13.
Vậy số từ giấy bạc loại 5000đ người ấy hoàn toàn có thể có là những số nguyên dương từ là 1 đến 13.
Bài 31 trang 48 sgk toán 8 tập 2
Giải những bất phương trình và màn biểu diễn tập nghiệm trên trục số:
a) (15 - 6x over 3 > 5)
b) (8 - 11x over 4 < 13)
c) (1 over 4left( x - 1 right) < x - 4 over 6)
d) (2 - x over 3 < 3 - 2x over 5)
Hướng dẫn làm bài:
a) (15 - 6x over 3 > 5 Leftrightarrow 15 - 6x > 15)
⇔-6x > 0
⇔x < 0
Vậy tập nghiệm là S =x/x<0.
Biểu diễn trên trục số:

b) (8 - 11x over 4 < 13 Leftrightarrow 8 - 11x < 52)
⇔-11x< 44
⇔x> -4
Vậy tập hợp nghiệm: x > -4
Biểu diễn trên trục số:

c) (1 over 4left( x - 1 right) < x - 4 over 6 Leftrightarrow 12.1 over 4left( x - 1 right) < 12.x - 4 over 6)
⇔3(x – 1) < 2 (x – 4) ⇔ 3x – 3 < 2x – 8
⇔3x – 2x < -8 + 3 ⇔ x < -5
Vậy tập hợp nghiệm : S = x/x < -5
Biểu diễn trên trục số:

d) (2 - x over 3 < 3 - 2x over 5 Leftrightarrow 15.2 - x over 3 < 15.3 - 2x over 5)
⇔5(2 – x) < 3(3 – 2x) ⇔ 10 – 5x < 9 – 6x
⇔6x – 5x < 9 – 10 ⇔ x < -1
Vậy tập nghiệm S = x/x < -1.
Biểu diện trên trục số:

Bài 32 trang 48 sgk toán 8 tập 2
Giải những bất phương trình:
a) 8x + 3(x + 1) > 5x – (2x – 6);
b)2x(6x – 1) > (3x – 2)(4x +3).
Hướng dẫn làm bài:
a)8x + 3(x + 1) > 5x – (2x – 6) ⇔ 8x + 3x + 3 > 5x – 2x + 6
⇔ 8x + 3 > 6
⇔8x > 3
⇔x > (3 over 8)
Vậy nghiệm của bất phương trình: x > (3 over 8)
b) 2x(6x – 1) > (3x – 2)(4x +3).
⇔12x2 – 2x > 12x2 – 8x + 9x – 6
⇔12x2 – 2x > 12x2 + x – 6
⇔-2x – x > - 6
⇔-3x > -6
⇔x < 2
Vậy nghiệm của bất phương trình là x < 2.
Bài 33 trang 48 sgk toán 8 tập 2
Đố: Trong một kì thi, bạn Chiến phải thi bốn môn Văn, Toán, Tiếng Anh và Hóa. Chiến đã thi ba môn và được kết quả như bảng sau:
Môn
Văn
Tiếng Anh
Hóa
Điểm
8
7
10
Kì thi quy định muốn đạt loại giỏi phải có điểm trung bình những môn thi là 8 trở lên và không còn môn nào bị điểm dưới 6. Biết môn Văn và Toán được xem thông số 2. Hãy cho biết thêm thêm, để đạt loại giỏi bạn Chiến phải có điểm thi môn Toán tối thiểu là bao nhiêu?
Hướng dẫn làm bài:
a) Gọi x là yếu tố thi môn Toán, theo đề bài ta có Đk:
6 ≤ x ≤ 10
Điểm trung bình của bốn môn:
(8.2 + 7 + 10 + x.2 over 6 = 33 + 2x over 6)
Để được xếp loại giỏi thì: (33 + 2x over 6 ge 8)
⇔33 + 2x ≥ 48
⇔2x ≥ 15
⇔x ≥ 7,5
Vậy để đạt được loại giỏi thì bạn Chiến phải có điểm thi môn Toán tối thiểu là 7.
Bài 34 trang 49 sgk toán 8 tập 2
Đố. Tìm sai lầm không mong muốn trong những “lời giải” sau:
a) Giải bất phương trình -2x > 23. Ta có:
-2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25.
b) Giải bất phương trình ( - 3 over 7x > 12) . Ta có:
( - 3 over 7x > 12 Leftrightarrow left( - 7 over 3 right).left( - 3 over 7 right) > left( - 7 over 3 right).12 Leftrightarrow x > - 28)
Vậy nghiệm của bất phương trình là x > -28.
Hướng dẫn làm bài:
a) -2x > 23 ⇔ x > 23 + 2 ⇔ x > 25.
Vậy nghiệm của bất phương trình là x > 25
Nhận xét: Sai lầm là: khi tìm x phải nhân hai vế với -(1 over 2) hoặc chia hai vế cho -2 và đổi chiều bất phương trình
Lời giải đúng: -2x > 23
⇔x < 23 : (-2)
⇔x < -11,5
Vậy nghiệm của bất phương trình: x < -11,5
b) ( - 3 over 7x > 12 Leftrightarrow left( - 7 over 3 right).left( - 3 over 7 right) > left( - 7 over 3 right).12 Leftrightarrow x > - 28)
Vậy nghiệm của bất phương trình là x > -28.
Nhận xét: Sai làm là nhân hai vế của bất phương trình cho mà không đổi chiều bất phương trình.
Lời giải đúng:
( - 3 over 7x > 12 Leftrightarrow left( - 7 over 3 right).left( - 3 over 7x right) < left( - 7 over 3 right).12)
⇔ x < -28
Vậy nghiệm của bất phương trình là x < -28.
Giaibaitap.me
Page 6
Bài 35 trang 51 sgk toán 8 tập 2
Bỏ dấu giá trị tuyệt đối và rút gọn những biểu thức:
a) A = 3x + 2 + |5x| trong hai trường hợp: x ≥ 0 và x < 0;
b) B = |4x| -2x + 12 trong hai trường hợp: x ≤ 0 và x > 0;
c) C = |x - 4| - 2x + 12 khi x > 5;
d) D = 3x + 2 + |x + 5|
Hướng dẫn giải:
a) A = 3x + 2 + |5x|
=> A = 3x + 2 + 5x khi x ≥ 0
A = 3x + 2 - 5x khi x < 0
Vậy A = 8x + 2 khi x ≥ 0
A = -2x + 2 khi x < 0
b) B = 4x - 2x + 12 khi x ≥ 0
B = -4x -2x + 12 khi x < 0
Vậy B = 2x + 12 khi x ≥ 0
B = -6x khi x < 0
c) Với x > 5 => x - 4 > 1 hay x - 4 dương nên
C = x - 4 - 2x + 12 = -x + 8
Vậy với x > 5 thì C = -x + 8
d) D= 3x + 2 + x+ 5 khi x + 5 ≥ 0
D = 3x + 2 - (x + 5) khi x + 5 < 0
Vậy D = 4x + 7 khi x ≥ -5
D = 2x - 3 khi x < -5
Bài 36 trang 51 sgk toán 8 tập 2
Giải những phương trình:
a) |2x| = x - 6; b) |-3x| = x - 8;
c) |4x| = 2x + 12; d) |-5x| - 16 = 3x.
Hướng dẫn giải:
a) |2x| = x - 6
|2x| = x - 6 ⇔ 2x = x - 6 khi x ≥ 0 ⇔ x = -6 không thoả mãn x ≥ 0
|2x| = x - 6 ⇔ -2x = x - 6 khi x < 0 ⇔ 3x = 6 ⇔ x = 2 không thoả mãn x < 0
Vậy phương trình vô nghiệm
b) |-3x| = x - 8
|-3x| = x - 8 ⇔ -3x = x - 8 khi -3x ≥ 0 ⇔ x ≤ 0
⇔ 4x = 8
⇔ x = 2 (không thoả mãn ≤ 0)
|-3x| = x - 8 ⇔ 3x = x - 8 khi -3x < 0 ⇔ x > 0
⇔ 2x = -8
⇔ x = -4 (không thoả mãn x < 0)
Vậy phương trình vô nghiệm
c) |4x| = 2x + 12
|4x| = 2x + 12 ⇔ 4x = 2x + 12 khi 4x ≥ 0 ⇔ x ≥ 0
⇔ 2x = 12
⇔ x = 6 (thoả mãn Đk x ≥ 0)
|4x| = 2x + 12 ⇔ -4x = 2x + 12 khi 4x < 0 ⇔ x < 0
⇔ 6x = -12
⇔ x = -2 (thoả mãn Đk x < 0)
Vậy phương trình có hai nghiệm x = 6 và x = -2
d) |-5x| - 16 = 3x
|-5x| - 16 = 3x ⇔ -5x - 16 = 3x khi -5x ≥ 0 ⇔ x ≤ 0
⇔ 8x = -16
⇔ x = -2 (thoả mãn Đk x ≤ 0)
|-5x| - 16 = 3x ⇔ 5x -16 = 3x khi -5x < 0 ⇔ x > 0
⇔ 2x = 16
⇔ x = 8 (thoả mãn Đk x > 0)
Vậy phương trình có hai nghiệm x = -2, x= 8
Bài 37 trang 51 sgk toán 8 tập 2
Giải những phương trình:
a) |x - 7| = 2x + 3; b) |x + 4| = 2x - 5;
c) |x + 3| = 3x - 1; d) |x - 4| + 3x = 5.
Hướng dẫn giải:
a) |x - 7| = 2x + 3
|x - 7| = 2x + 3 ⇔ x - 7 = 2x + 3 khi x - 7 ≥ 0 ⇔ x ≥ 7
⇔ x = -10 (không thoả mãn Đk x ≥ 7)
|x - 7| = 2x + 3 ⇔ -x + 7 = 2x + 3 khi x - 7 < 0 ⇔ x < 7
⇔ 3x = 4
⇔ x = ( frac43) (thoả mãn Đk x < 7)
Vậy phương trình có nghiệm x = ( frac43)
b) |x + 4| = 2x - 5 ⇔ x + 4 = 2x - 5 khi x + 4 ≥ 0 ⇔ x ≥ -4
⇔ x = 9 ( thoả mãn Đk x ≥ -4)
|x + 4| = 2x - 5 ⇔ -x - 4 = 2x - 5 khi x + 4 < 0 ⇔ x < -4
⇔ 3x = 1
⇔ x = ( frac13) (không thoả mãn Đk x < -4)
Vậy phương trình có nghiệm x = 9
c) |x + 3| = 3x - 1
|x + 3| = 3x - 1 ⇔ x + 3 = 3x - 1 khi x + 3 ≥ 0 ⇔ x ≥ -3
⇔ 3x = 4
⇔ x = ( frac43) (thoả mãn Đk x ≥ -3)
|x + 3| = 3x - 1 ⇔ -x - 3 = 3x - 1 khi x < -3
⇔ 4x = -2
⇔ x = ( -frac12) (không thoả mãn Đk x < -3)
Vậy phương trình có nghiệm x = ( frac43)
d) |x - 4| + 3x = 5
|x - 4| + 3x = 5 ⇔ x - 4 + 3x = 5 khi x ≥ 4
⇔ 4x = 9
⇔ x = ( frac94) (không thoả mãn Đk x ≥ 4)
|x - 4| + 3x = 5 ⇔ -x + 4 + 3x = 5 khi x < 4
⇔ 2x = 1
⇔ x = ( frac12)
Giaibaitap.me
Page 7
Bài 38 trang 53 sgk toán 8 tập 2
Cho m > n, chứng tỏ:
a)m + 2 > n +2; b)-2m < -2n;
c)2m – 5 > 2n – 5; d)4 – 3m < 4 – 3n.
Hướng dẫn làm bài:
a) Ta có m > n => m + 2 > n + 2 (cộng vào hai vế với 2)
b) Ta có m > n => - 2m < - 2n (nhân vào hai vế với -2)
c) m > n => 2m > 2n (nhân hai vế với 2)
=>2m – 5 > 2n – 5 (cộng vào hai vế với -2)
d) m > n => -3m < -3n (nhân hai vế với -3)
=>4 – 3m < 4 – 3n (cộng vào hai vế với 4)
Bài 39 trang 53 sgk toán 8 tập 2
Kiểm tra xem -2 là nghiệm của bất phương trình nào trong những bất phương trình sau:
a)-3x + 2 > -5; b)10 – 2x < 2;
c)x2 – 5 < 1; d)|x| < 3;
e)|x| > 2; f)x + 1 > 7 – 2x.
Hướng dẫn làm bài:
a)Thay x = -2 vào bất phương trình: -3x + 2 > -5
-3 (-2) + 2 > -5 ⇔ 6 +2 > -5 ⇔ 8 > -5 (xác lập đúng).
Vậy x = -2 là nghiệm của -3x + 2 > -5
b)Thay x = -2 vào bất phương trình: 10 – 2x < 2 được
10 – 2(-2) < 2 ⇔ 10 + 4 < 2 ⇔ 14 < 2 (sai)
c)Thay x = -2 vào bất phương trình x2 – 5 < 1 được
(-2)2 – 5 < 1 ⇔ 4 – 5 < 1 ⇔ -1 < 1 (đúng)
Vậy x = -2 là nghiệm của x2 – 5 < 1
d)Thay x = -2 vào bất phương trình |x | < 2 được
|-2| < 3 ⇔ 2 < 3 (đúng)
Vậy x = -2 là nghiệm của |x| < 3.
e)Thay x = -2 vào bất phương trình |x| > 2 được
|-2| > 2 ⇔ 2 > 2 (sai)
Vậy x = -2 không là nghiệm của |x| > 2.
f)Thay x = -2 vào bất phương trình x + 1 > 7 – 2x được
(-2) + 1 > 7 – 2(-2) ⇔ -1 > 11 (sai)
Vậy x = -2 không là nghiệm của x + 1 > 7 – 2x
Bài 40 trang 53 sgk toán 8 tập 2
Giải những bất phương trình và màn biểu diễn tập nghiệm trên trục số:
a) x – 1 < 3; b) x + 2 > 1;
c) 0,2x < 0,6; d) 4 + 2x < 5.
Hướng dẫn làm bài:
a)x – 1 < 3 ⇔ x < 1 + 3 ⇔ x < 4
Vậy tập nghiệm S = x/x <4
Biểu diễn trên trục số

b)x +2 > 1 ⇔ x > 1 – 2 ⇔ x > -1
Vậy tập nghiệm S = x/x > -1.
Biểu diễn trên trục số

c)0,2x < 0,6 ⇔ 5.0,2x < 5.0,6 ⇔ x < 3
Vậy tập nghiệm S = x/x < 3.
Biểu diễn trên trục số

d)4 +2x < 5 ⇔ 2x < 5 – 4 ⇔ x <
Vậy tập nghiệm S =x/ x <
Biểu diễn trên trục số

Bài 41 trang 53 sgk toán 8 tập 2
Giải những bất phương trình:
a) (2 - x over 4 < 5;)
b)(3 le 2x + 3 over 5a)
c) (4x - 5 over 3 > 7 - x over 5) ;
d)(2x + 3 over - 4 ge 4 - x over - 3) .
Hướng dẫn làm bài:
a) (2 - x over 4 < 5 Leftrightarrow 2 - xleftlangle 20 Leftrightarrow x rightrangle - 18)
Vậy nghiệm của bất phương trình: x > -18
b) (3 le 2x + 3 over 5 Leftrightarrow 15 le 2x + 3)
⇔(15 - 3 le 2x Leftrightarrow 12 le 2x Leftrightarrow 6 le x)
Vậy nghiệm của bất phương trình: (x ge 6)
c) (4x - 5 over 3 > 7 - x over 5 Leftrightarrow 5left( 4x - 5 right) > 3left( 7 - x right))
⇔20 x – 25 > 21 – 3x
⇔23x > 46
⇔x > 2
Vậy nghiệm của bất phương trình: x > 2
d) (2x + 3 over - 4 ge 4 - x over - 3 Leftrightarrow left( - 12 right)left( 2x + 3 over - 4 right) le left( - 12 right)left( 4 - x over - 3 right))
⇔3(2x + 3) ≤ 4(4 – x) ⇔ 6x + 9 ≤ 16 – 4x
⇔6x + 4x ≤ 16 – 9 ⇔ 10x ≤ 7
⇔(x le 7 over 10)
Vậy nghiệm của bất phương trình là (x le 7 over 10)
Giaibaitap.me
Page 8
Bài 42 trang 53 sgk toán 8 tập 2
Giải những bất phương trình:
a) 3 – 2x > 4; b) 3x + 4 < 2;
c) (x – 3)2 < x2 – 3; d) (x-3)(x+3) < (x+2)2 + 3.
Hướng dẫn làm bài:
a)3 – 2x > 4 ⇔ 3 – 4 > 2x ⇔ -1 > 2x
⇔( - 1 over 2 > x)
Vậy nghiệm của bất phương trình: (x < - 1 over 2)
b)3x + 4 < 2 ⇔3x < 2 – 4 ⇔ 3x < -2 ⇔(x < - 2 over 3)
Vậy nghiệm của bất phương trình:(x < - 2 over 3)
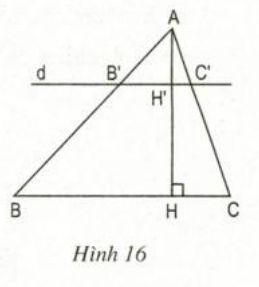
c)(x – 3)2 < x2 – 3 ⇔x2 – 6x + 9 ⇔x2 – 6x – x2 < -3 – 9 ⇔-6x < -12 ⇔x > 2 Vậy nghiệm của bất phương trình : x > 2 d)(x-3)(x+3) < (x+2)2 + 3 ⇔ x2 – 9 < x2 + 4x + 4 +3 ⇔x2 – x2 – 4x < 4 + 3 + 9 ⇔-4x < 16 ⇔x > -4 Vậy nghiệm của bất phương trình x > -4. Bài 43 trang 53 sgk toán 8 tập 2 Tìm x sao cho: a) Giá trị của biểu thức 5 – 2x là số dương; b) Giá trị của biểu thức x + 3 nhỏ hơn giá trị của biểu thức 4x – 5; c) Giá trị của biểu thức 2x +1 không nhỏ hơn giá trị của biểu thức x + 3; d) Giá trị của biểu thức x2 +1 không to nhiều hơn giá trị của biểu thức (x – 2)2. Hướng dẫn làm bài: a) Ta có bất phương trình 5 – 2x > 0. ⇔5 > 2x ⇔ x < (5 over 2). b) Ta có bất phương trình : x + 3 < 4x – 5 ⇔x – 4x < -5 – 3 ⇔-3x < -8 ⇔x > (8 over 3) Vậy khiến cho x + 3 nhỏ hơn 4x – 5 thì x >(8 over 3) . c) Ta có bất phương trình : 2x +1 ≥ x + 3 ⇔ 2x – x ≥ 3 – 1 ⇔ x ≥ 2 Vậy khiến cho 2x +1 không nhỏ hơn x + 3 thì x ≥ 2 d) Ta có bất phương trình : x2 + 1 ≤ (x – 2)2 ⇔ x2 + 1 ≤ x2 – 4x + 4 ⇔x2 – x2 + 4x ≤ 4 – 1 ⇔4x ≤ 3 ⇔(x le 3 over 4) Vậy để cho giá trị của x2 + 1 không to nhiều hơn giá trị của (x – 2)2 thì (x le 3 over 4) Bài 44 trang 54 sgk toán 8 tập 2 Đố. Trong một cuộc thi đố vui. Ban tổ chức triển khai quy định từng người tham gia cuộc thi phải vấn đáp 10 vướng mắc ở vòng sơ tuyển. Mỗi vướng mắc này còn có sẵn 4 đáp án, nhưng trong số đó chỉ có một đáp án đúng. Người tham gia cuộc thi chọn đáp án đúng sẽ tiến hành 5 điểm, chọn đáp án sai sẽ bị trừ đi 1 điểm. Ở vòng sơ tuyển, Ban tổ chức triển khai tặng cho từng người tham gia cuộc thi 10 điểm và quy định người nào có tổng số điểm từ 40 trở lên mới được tham gia cuộc thi ở vòng tiếp theo. Hỏi người tham gia cuộc thi phải vấn đáp đúng chuẩn bao nhiêu vướng mắc ở vong sơ tuyển thì mới được tham gia cuộc thi tiếp ở vòng sau? Hướng dẫn làm bài: Gọi x là số câu vấn đáp đúng Số câu vấn đáp sai: 10 – x Sau khi vấn đáp 10 câu thì người tham gia cuộc thi sẽ có được: 5x – (10 – x) + 10 Để được tham gia cuộc thi tiếp vòng sau thì 5x – (10 – x ) +10 ≥ 40 ⇔ 5x - 10 + x + 10 ≥ 40 ⇔6x ≥ 40 ⇔ x ≥(20 over 3) Vì x là số nguyên dương nhỏ hơn hay bằng 10 nên (20 over 3 le x le 10) Vậy người tham gia cuộc thi phải vấn đáp đúng chuẩn tối thiểu 7 vướng mắc thì mới được tham gia cuộc thi tiếp ở vòng sau. Bài 45 trang 54 sgk toán 8 tập 2 Giải những phương trình: a)|3x| = x + 8; b)|-2x| = 4x + 18; c)|x – 5| = 3x; d)|x + 2| = 2x – 10. Hướng dẫn làm bài: a)|3x| = x + 8 ⇔(left[ matrix3x = x + 8;x ge 0 cr - 3x = x + 8;x < 0 cr right.) ⇔(left[ matrix2x = 8 cr - 4x = 8 cr right.) ⇔(left[ matrixx = 4 ; cr x = - 2 ; cr right.) x = 4 thỏa mãn nhu cầu ĐK x ≥ 0 và x = -2 thỏa mãn nhu cầu ĐK x < 0 Vậy tập hợp nghiệm S = 4;-2 b)|-2x| = 4x + 18 vì |-2x| = |2x| ⇔ |2x| = 4x +18 ⇔ (left[ matrix2x = 4x + 18;x ge 0 cr - 2x = 4x + 18;x < 0 cr right. Leftrightarrow left[ matrix - 2x = 18 cr - 6x = 18 cr right.) ⇔(left[ matrixx = - 9; cr x = - 3 cr right.) x = -9 không thỏa mãn nhu cầu ĐK x ≥ 0 Vậy phương trình có tập nghiệm S = -3 c)|x – 5| = 3x ⇔(left[ matrixx - 5 = 3x;x ge 5 cr - x + 5 = 3x;x < 5 cr right.) ⇔(left[ matrix - 5 = 2x cr 5 = 4x cr right.) ⇔(left[ matrixx = - 5 over 2 cr x = 5 over 4 cr right.) (x = - 5 over 2) không thỏa mãn nhu cầu ĐK x ≥ 5 Vậy tập hợp nghiệm của phương trình (S = left 5 over 4 right\) d) |x + 2| = 2x – 10. ⇔(left[ matrixx + 2 = 2x - 10;x ge - 2 cr - x - 2 = 2x - 10;x < - 2 cr right.) ⇔(left[ matrixx = 12 cr x = 8 over 3 cr right.) (x = 8 over 3) không thỏa mãn nhu cầu Đk x < -2 Vậy tập hợp nghiệm của phương trình S =12 Giaibaitap.me Bài 6 trang 62 - Sách giáo khoa toán 8 tập 2 Tìm những cặp đường thẳng tuy nhiên tuy nhiên trong hình 13 và lý giải vì sao chúng tuy nhiên tuy nhiên. Giải: Trên hình 13a ta có: (fracAPPB) = (frac38); (fracAMMC)= (frac515) = (frac13) vì (frac38) ≠ (frac13) nên (fracAPPB) ≠ (fracAMMC) => PM và MC không tuy nhiên tuy nhiên. Ta có (left.beginmatrix &fracCNNB=frac217=3 \ & fracCMMA=frac155=3 endmatrixright} => fracCMMA=fracCNNB) => MN//AB Trong hình 13b Ta có: (fracOA'A'A) = (frac23); (fracOB'B'B) = (frac34,5) = (frac23) => (fracOA'A'A) = (fracOB'B'B) => A'B' // AB (1) Mà (widehatB"A"O) = (widehatOA'B') lại so le trong Suy ra A"B" // A'B' (2) Từ 1 và 2 suy ra AB // A'B' // A"B" Bài 7 trang 62 - Sách giáo khoa toán 8 tập 2 Tính những độ dài x,y trong hình 14. Giải: * Trong hình 14a MN // EF => (fracMNEF) = (fracMDDE) mà DE = MD + ME = 9.5 + 28 = 37.5 Nên (frac8x) = (frac9,537,5) => x= (frac8.37.59.5) = (frac60019) ≈ 31,6 * Trong hình 14b Ta có A'B' ⊥ AA'(gt) và AB ⊥ AA'(gt) => A'B' // AB => (fracA'OOA) = (fracA'B'AB) hay (frac36) = (frac4,2x) x = (frac6.4,23) = 8.4 ∆ABO vuông tại A => OB2 = y2 = OA2 + AB2 => y2 = 62+ 8,42 => y2 = 106,56 => y ≈ 10,3 Bài 8 trang 63 - Sách giáo khoa toán 8 tập 2 a) Để chi đoạn thẳng AB thành ba đoạn bằng nhau, người ta đã làm như hình 15. Hãy mô tả cách làm trên và lý giải vì sao những đoạn AC,CD,DB bằng nhau? b) Bằng cách tương tự, hãy chi đoạn thẳng AB cho trước thành 5 đoạn bằng nhau. Hỏi có cách nào khác với cách làm trên mà vẫn hoàn toàn có thể chia đoạn AB cho trước thành 5 đoạn bằng nhau? Giải: a) Mô tả cách làm: Vẽ đoạn PQ tuy nhiên tuy nhiên với AB. PQ có độ dài bằng 3 cty - Xác định giao điểm O của hai đoạn thẳng PB và QA. - Vẽ những đường thẳng EO, FO cắt AB tại C và D. Chứng minh AC=CD=DB ∆OPE và ∆OBD có PE//DB nên (fracDBPE) = (fracODOE) (1) ∆OEF và ∆ODC có PE // CD nên (fracCDEF) = (fracODOE) (2) Từ 1 và 2 suy ra: (fracDBPE) = (fracCDEF) mà PE = EF nên DB = CD. Chứng minh tương tự: (fracACDF) = (fracCDEF) nên AC = CD. Vây: DB = CD = AC. b) Tương tự chia đoạn thẳng AB thành 5 đoạn bằng nhau thực thi như hình vẽ sau: Ta hoàn toàn có thể chia đoạn thẳng AB thành 5 đoạn thẳng bằng nhau như cách sau: Vẽ 6 đường thẳng tuy nhiên tuy nhiên cách đều nhau( hoàn toàn có thể dùng thước kẻ để vẽ liên tục). Đặt đầu mút A và B ở hai tuyến phố thẳng ngoài cùng thì những đường thẳng tuy nhiên tuy nhiên căt AB phân thành 5 phần bằng nhau. Bài 9 trang 63 - Sách giáo khoa toán 8 tập 2 Cho tam giác ABC và điểm D trên cạnh AB sao cho AD= 13,5cm, DB= 4,5cm. Tính tỉ số những khoảng chừng cách tự điểm A và B đến cạnh AC Giải: Gọi DH và BK lần lượt là khoảng chừng cách từ B và D đến cạnh AC. Ta có DH // BK (cùng vuông góc với AC) => (fracDHBK) = (fracADAB) Mà AB = AD + DB => AB = 13,5 + 4,5 = 18 (cm) Vậy (fracDHBK) = (frac13,518) = (frac34) Vậy tỉ số khoảng chừng cách từ điểm D và B đến AC bằng (frac34) Bài 10 trang 63 - Sách giáo khoa toán 8 tập 2 Tam giác ABC có đường cao AH. Đường thẳng d tuy nhiên tuy nhiên với BC, cắt những cạnh AB,AC và đường cao AH theo thứ tự tại những điểm B', C' và H'(h.16) a) Chứng minh rằng: (fracAH'AH) = (fracB'C'BC). b) Áp dụng: Cho biết AH' = (frac13) AH và diện tích s quy hoạnh tam giác ABC là 67.5 cm2 Tính diện tích s quy hoạnh tam giác AB'C'. Giải: a) Chứng minh (fracAH'AH) = (fracB'C'BC) Vì B'C' // với BC => (fracB'C'BC) = (fracAB'AB) (1) Trong ∆ABH có BH' // BH => (fracAH'AH) = (fracAB'BC) (2) Từ 1 và 2 => (fracB'C'BC) = (fracAH'AH) b) B'C' // BC mà AH ⊥ BC nên AH' ⊥ B'C' hay AH' là đường cao của tam giác AB'C'. Áp dụng kết quả câu a) ta có: AH' = (frac13) AH (fracB'C'BC) = (fracAH'AH) = (frac13) => B'C' = (frac13) BC => SAB’C’= (frac12) AH'.B'C' = (frac12).(frac13)AH.(frac13)BC =>SAB’C’= ((frac12)AH.BC)(frac19) mà SABC= (frac12)AH.BC = 67,5 cm2 Vậy SAB’C’= (frac19).67,5= 7,5 cm2 Giaibaitap.me Bài 11 trang 63 - Sách giáo khoa toán 8 tập 2 Tam giác ABC có BC= 15cm. Trên đường cao AH lấy những điểm I,K sao cho AK = KI = IH. Qua I và K vẽ những đường EF // BC, MN // BC(h.17) a) Tính độ dài đoạn MN và EF. b) Tính diện tích s quy hoạnh tứ giác MNFE, biết diện tích s quy hoạnh của tam giác ABC là 270 cm2 Giải: a) ∆ABC có MN // BC. => (fracMNCB) = (fracAKAH)(kết quả bài tập 10) Mà AK = KI = IH Nên (fracAKAH) = (frac13) => (fracMNCB) = (frac13) => MN = (frac13)BC = (frac13).15 = 5 cm. ∆ABC có EF // BC => (fracEFBC) = (fracAIAH) = (frac23) => EF = (frac23).15 =10 cm. b) Áp dụng kết quả ở câu b của bài 10 ta có: SAMN= (frac19).SABC= 30 cm2 SAEF= (frac49).SABC= 120 cm2 Do đó SMNEF = SAEF - SAMN = 90 cm2 Bài 12 trang 64 - Sách giáo khoa toán 8 tập 2 Có thể đo dược chiều rông của một khúc sông mà tránh việc phải sang bờ bên kia hay là không? Người ta tiền hành đo đạc những yếu tố hình học thiết yếu để tình chiều rộng của khúc sông mà tránh việc phải sang bờ bên kia(h18). Nhìn hình vẽ, Hãy mô tả những việc làm cần làm và tính khoảng chừng cách AB=x theo BC=a a, B'C'= a', BB'= h. Giải: mô tả cách làm: * Chọn một điểm A cố định và thắt chặt bên mép bờ sông bên kia( ví như thể một thân cây), đặt hai điểm B và B' thẳng hàng với A, điểm B sát mép bờ còn sót lại và AB chình là khoảng chừng cách cần đo. * Trên hai tuyến phố thẳng vuông góc với AB' tại B và B' lấy C và C' thẳng hàng với A. * Đo độ dài những đoạn BB'= h, BC= a, B'B'= a'. Giải Ta có: (fracABAB') = (fracBCBC') mà AB' = x + h nên (fracxx+ h) = (fracaa') <=> a'x = ax + ah <=> a'x - ax = ah <=> x(a' - a) = ah x= (fracaha'-a) Vậy khoảng chừng cách AB bằng (fracaha'-a) Bài 13 trang 64 - Sách giáo khoa toán 8 tập 2 Có thể đo gián tiếp độ cao của một bức tường bằng dụng cụ do đơn thuần và giản dị được không? Hình 19: thể hiện cách đo độ cao AB của một bức tường bằng những dụng cụ đơn thuần và giản dị gồm: Hai cọc thẳng đứng và sợi dây FC, Cọc 1 có độ cao DK= h. Các khoảng chừng cách BC= a, DC= b đo được bằng thước thông dụng. a) Em hay cho biết thêm thêm người ta tiến hành đo đạc ra làm sao ? b) Tính độ cao AB theo h, a, b. a) Cách tiến hành: - Đặt hai cọc thẳng đứng, di tán cọc 2 sao cho 3 điểm A,F,K nằm trên đường thẳng. - Dùng sợi dây căng thẳng mệt mỏi qua 2 điểm F và K để xác lập điểm C trên mặt đất( 3 điểm F,K,C thẳng hàng). b) ∆BC có AB // EF nên (fracEFAB) = (fracECBC) => AB = (fracEF.BCEC) = (frach.ab) Vậy độ cao của bức tường là: AB = (frach.ab). Bài 14 trang 64 - Sách giáo khoa toán 8 tập 2 Cho ba đoạn thẳng có độ dài là m,n,p.( cùng cty đo). Dựng đoạn thẳng có độ dài x sao cho: a) (fracxm)= 2; b) (fracxn) = (frac23); c) (fracmx) = (fracnp.) Giải: a) Cách dựng: - Vẽ hai tia Ox, Oy không đối nhau. - Trên tia Oy đặt điểm B sao cho OB = 2 cty. - Lấy trung điểm của OB, - Nối MA. - Vẽ đường thẳng trải qua B và tuy nhiên tuy nhiên với MA cắt Ox tại C thì (fracOCOA) = (fracOBOM); OB = 2 OM => (fracxm) = 2 b) Cách dựng: - Vẽ hai tia Ox và Oy không đối nhau. - Trên tia Ox đặt hai đoạn OA= 2 cty, OB= 3 cty. - Trên tia Oy đặt đoạn OB' = n - Nối BB' - Vẽ đường thẳng qua A tuy nhiên tuy nhiên với BB' cắt Oy tại A' và OA' = x. Ta có: AA' // BB' => (fracOA'OB') = (fracOAOB) hay (fracxn) = (frac23) c) Cách dựng: - Vẽ tia Ox, Oy không đối nhau. - Trên tia Ox đặt đoạn OA= m, OB= n. - Trên tia Oy đặt đoạn OB' = p.. - Vẽ đường thẳng qua A và tuy nhiên tuy nhiên với BB' cắt Oy tại A' thì OA' = x. Thật vậy: AA' // BB' => (fracOAx) = (fracOBOB') hay (fracmx) = (fracnp.) Giaibaitap.me Bài 35 trang 79 - Sách giáo khoa toán 8 tập 2 Chứng minh rằng nếu tam giác (A'B'C') đồng dạng với tam giác (ABC) theo tỉ số (k) thì tỉ số của hai tuyến phố phân giác tương ứng của chúng cũng bằng (k). Giải: (∆A'B'C' ∽ ∆ABC) theo tỉ số (k= fracA'B'AB) ( Rightarrow widehat BAC = widehat B'A'C') (1) (AD) là phân giác góc (widehat BAC) nên (widehat BAD = 1 over 2widehat BAC) (2) (A'D') là phân giác góc (widehat B'A'C') nên (widehat B'A'D' = 1 over 2widehat B'A'C') (3) Từ (1),(2) và (3) suy ra: (widehatBAD) = (widehatB'A'D') Xét (∆A'B'D') và (∆ABD) có: +) (widehatB) = (widehatB') +) (widehatBAD) = (widehatB'A'D') (Rightarrow ∆A'B'D' ∽ ∆ABD) theo tỉ số ( fracA'B'AB)= (fracA'D'AD=k) Bài 36 trang 79 - Sách giáo khoa toán 8 tập 2 Tính độ dài x của đường thẳng BD trong hình 43(Làm tròn đến chữ thập phân thứ nhất), biết rằng ABCD là hinh thang(AD // CD); AB= 12,5cm; CD= 28,5cm (widehatDAB) = (widehatDBC). Giải xét ∆ABD và ∆BDC có: (widehatDBC) = (widehatDBC)(gt) (widehatABD) = (widehatBDC) => ∆ABD ∽ ∆BDC(trường hợp 3) => (fracABBD) = (fracDBDC) => BD2 = AB.DC => BD = √(AB.DC) = √(12,5.8,5) => BD = 10,3 cm Bài 37 trang 79 - Sách giáo khoa toán 8 tập 2 Hình 44 cho biết thêm thêm (widehatEBA) = (widehatBDC). a) Trong hình vẽ, có bao nhiêu tam giác vuông? Hãy kể tên những tam giác đó. b) Cho biết AE = 10cm, AB = 15cm, BC = 12cn, Hãy tính độ dài những đoạn thẳng CD, BE, BD, ED(làm tròn đén chữ số thập phân thứ nhất). c) So sánh diện tích s quy hoạnh tam giác BDE với tổng diện tích s quy hoạnh hai tam giác AEB và BCD. Giải: (widehatEBA) = (widehatBDC).(gt) mà (widehatBCD) + (widehatCBD) = 900 => (widehatEBA) + (widehatCBD) = 900 Vậy (widehatEBD) = 900 Vậy trong hình vẽ có ba tam giác vuông đó là: ∆ABE, ∆CBD, ∆EBD. b) ∆ABE và ∆CDB có: (widehatA) = (widehatC) = 900 (widehatABE) = (widehatCDB) => ∆ABE ∽ ∆CDB => (fracABCD) = (fracAECB) => CD = (fracAB.CBAE) = 18 (cm) ∆ABE vuông tại A => BE = (sqrtAE^2+AB^2) = (sqrt10^2+15^2) = 21,6 (cm). ∆EBD vuông tại B => ED = (sqrtEB^2+BD^2) = (sqrt325+ 468) = 28.2 (cm) c) Ta có: (S_ABE) + (S_DBC) = (frac12)AE.AB + (frac12)BC.CD = (frac12). 10.15 + (frac12)12.18 = 75 + 108 = 183 cm2 (S_ACDE)= (frac12)(AE + CD).AC = (frac12)(10 + 18).27= 378 cm2 => (S_EBD)= (S_EBD) - ((S_ABE) + (S_DBC)) = 378 - 183 = 195cm2 (S_EBD)> (S_ABE) + (S_DBC) Bài 38 trang 79 - Sách giáo khoa toán 8 tập 2 Tính độ dài x,y của những đoạn thẳng trong hình 45. Giải: (widehatABD) = (widehatBDE), lại so le trong => AB // DE => ∆ABC ∽ ∆EDC => (fracABED) = (fracBCDC) = (fracACEC) => (frac36) = (fracx3,5) = (frac2y) => x = (frac3. 3,56) = 1.75; y = (frac6.23) = 4 Giaibaitap.me Bài 43 trang 80 - Sách giáo khoa toán 8 tập 2 Cho hình bình hành ABCD(h46) có độ dài những cạnh AB = 12cm, BC = 7cm. Trên cạnh AB lấy một điểm E sao cho AE = 8cm. Đường thẳng DE cắt CB kéo dãn tại F, a) Trong hình vẽ đã cho có bao nhiêu cặp tam giác đồng dạng? hãy viết những cặp tam giác đồng dạng với nhau theo những đỉnh tương ứng. b) Tính độ dài đoạn EF và BF, biết rằng DE = 10cm. Giải: a) BE // DC => ∆BEF ∽ ∆CDF AD // BF => ∆ADE ∽ ∆BFE. Do đó: ∆ADE ∽ ∆CFD b) BE = AB - AE = 12 - 8 = 4cm ∆ADE ∽ ∆BFE => (fracAEBE) = (fracADBF) = (fracDEEF) => (frac84) = (frac7BF) = (frac10EF) => BF = 3,5 cm. EF = 5 cm. Bài 44 trang 80 - Sách giáo khoa toán 8 tập 2 Cho tam giác ABC có những cạnh AB= 24cm, AC = 28cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M,N theo thứ tự là hình chiếu của B và C trên AD. a) Tính tỉ số (fracBMCN) b) Chứng minh rằng (fracAMAN) = (fracDMDN) Giải: a) AD là đường phân giác của ∆ABC => (fracDBDC) = (fracABAC) = (fracDBDC) = (frac2428) = (frac67) Mà BM // CN (cùng vuông góc với AD). => ∆BMD ∽ ∆CND => (fracBMCN) = (fracBDCD) Vậy (fracBMCN) = (frac67) b) ∆ABM và ∆ACN có: (widehatABM) = (widehatCAN) (widehatBMA) = (widehatCNA) = 900 => ∆ABM ∽ ∆ACN => (fracAMAN) = (fracABAC). mà (fracABAC) = (fracDBDC) (cmt) và (fracBDCD) = (fracDMDN) => (fracAMAN) = (fracDMDN) Bài 44 trang 80 sgk toán 8 tập 2 Cho tam giác ABC có những cạnh AB = 24 cm, AC = 28 cm. Tia phân giác của góc A cắt cạnh BC tại D. Gọi M, N theo thứ tự là hình chiếu của B và C trên đường thẳng AD. a)Tính tỉ số (BM over CN). b)Chứng minh rằng (AM over AN = DM over DN) . Hướng dẫn làm bài: a) AD là đường phân giác trong ∆ABC =>(DB over DC = AB over AC = > DB over DC = 24 over 28 = 6 over 7) Mà BM // CN (cùng vuông góc với AD). =>∆BMD ∽ ∆CND =>(BM over CN = BD over CD) Vậy:(BM over CN = 6 over 7) b) ∆ABM và ∆CAN có: (widehat BAM = widehat CAN) (AD là phân giác (widehat BAC) ) (widehat BMA = widehat CNA = 90^0) =>∆ABM ∽∆ACN =>(AM over AN = AB over AC) Mà (AB over AC = DB over DC) (chứng tỏ trên) Và (DB over DC = DM over DN) (∆BMD ∽∆CND) =>(AM over AN = DM over DN) Bài 45 trang 80 - Sách giáo khoa toán 8 tập 2 Hai tam giác ABC và DEF có (widehatA) = (widehatD), (widehatB) = (widehatE), AB = 8cm, BC = 10cm, DE= 8cm. Tính độ dài những cạnh AC, DF và EF, biết rằng cạnh AC dài hơn thế nữa cạnh DF là 3cm. Giải: ∆ABC ∽ ∆DEF vì có (widehatA) = (widehatD), (widehatB) = (widehatE) nên đồng dạng. Vì ∆ABC ∽ ∆DEF => (fracABDE) = (fracBCEF) = (fracCAFD) Hay (frac86) = (frac10EF) = (fracCAFD) Suy ra: EF = 7,5 cm Vì (frac86) = (fracCAFD) => (fracCA8) = (fracFD6) = (fracCA - FD8-6) = 3/2 => CD = (frac8.32) = 12 cm FD = 12 -3 = 9cm Giaibaitap.me Bài 46 trang 84 - Sách giáo khoa toán 8 tập 2 Trên hình 50, hãy chỉ ra những tam giác đồng dạng. Viết những tam giác này theo thứ tự đỉnh tương ứng và lý giải vì sao chúng đồng dạng? Giải ∆ADC ∽ ∆ABE vì góc A chung và (widehatD) = (widehatB) = 900 ∆DEF ∆BCF vì (widehatD) = (widehatB) = 900 , ( widehatDEF) = ( widehatBFC) ∆DFE ∆BAE vì ( (widehatD) = (widehatB) = 900 , góc A chung) ∆BFC ∆DAC vì ((widehatD) = (widehatB) = 900, góc C chung) Bài 47 trang 84 - Sách giáo khoa toán 8 tập 2 Tam giác ABC có độ dài những cạnh là 3cm, 4cm, 5cm. Tam giác A'B'C' đồng dạng với tam giác ABC và có diện tích s quy hoạnh là 54 cm2 Tính độ dài cách cạnh của tam giác A'B'C'. Giải: Vì ∆ABC ∽ ∆A'B'C' => ( fracS_ABCS_A'B'C') = ( (fracABA'B')^2) mà ∆ABC có độ dài những cạnh là 3,4,5 nên là tam giác vuông Suy ra: ( S_ABC) = ( frac12).3.4= 6 Do đó: ( frac654) = ( (fracABA'B')^2) <=> ( (fracABA'B')^2) = ( frac19) => ( fracABA'B') = ( frac13). => A'B' = 3 AB = 3.3 Tức là mỗi cạnh của tam giác A'B'C' gấp 3 lần của cạnh của tam giác ABC. Vậy ba cạnh của tam giác A'B'C là 9cm, 12cm, 15cm. Bài 48 trang 84 - Sách giáo khoa toán 8 tập 2 Bóng của một cột điện trên mặt đất có độ dài là 4.5m. Cùng thời gian lúc đó, một thanh sắt cao 2,1m cắm vuông góc với mặt đất có bóng dài 0,6m. Tính độ cao của cột điện. Giải: Cùng thuở nào điểm tia nằng mặt trời và mặt nhất bằng nhau nên hai tam giác vuông ∆ABC và ∆A'B'C' đồng dạng. ∆ABC ∽ ∆A'B'C => ( fracABA'B') = ( fracACA'C') => AB = ( fracAC.A'B'A'C') => AB = ( frac4,5.2,10,6) = 15,75 m Bài 49 trang 84 - Sách giáo khoa toán 8 tập 2 Ở hình 51, tam giác ABC vuông tại A có đường cao AH a) Trong hình vẽ có bao nhiêu cặp tam giác đồng dạng?. b) Cho biết: AB = 12,45 cm, AC = 20,50cm. Tính độ dài những đoạn BC, AH, BH và CH. Giải: a) ∆ABC ∽ ∆HBA vì ( widehatA) = ( widehatH) = 900 ,( widehatB) chung ∆ABC ∽ ∆HAC vì ( widehatA) = ( widehatH) = 900, ( widehatC) chung b) ∆ABC vuông tại A => BC2 = AB2 + AC2 => BC2 = 12,452 + 20,502 = 575,2525 => BC= √575,2525 ≈ 24 cm ∆ABC ∽ ∆HBA => ( fracABHB) = ( fracBCBA) => HB = ( fracAB^2BC) ≈ ( frac12,45^224) ≈ 6,5 cm => CH = BC - BH = 24 - 6,5 ≈ 17,5 cm. Mặt khác: ( fracACAH) = ( fracAB.ACBC) = ( frac12,45.20,2524) => AH = 10,6 cm Bài 50 trang 84 - Sách giáo khoa toán 8 tập 2 Bóng của một ống khói nhà máy sản xuất trên mặt đất có độ dài 36,9m. Cùng thời gian lúc đó, một thanh sắt cao 2,1 m cắm vuông góc với mặt đất có bóng dài 1,62m. Tính độ cao của ống khói. Giải: Tương tự bài 48. ∆ABC ∽ ∆A'B'C' ( fracABA'B') = ( fracACA'C') => ( AB= fracA'B'.ACA'C') => ( AB= frac36,9.2,11,62) => AB ≈ 47,8m Bài 51 trang 84 - Sách giáo khoa toán 8 tập 2 Chân đường cao AH của tam giác vuông ABC chia cạnh huyền BC thành hai đoạn có độ dài 25cm và 36cm. Tính chu vi và diện tích s quy hoạnh của tam giác vuông đó(h.53) Hướng dẫn: Trước tiên tìm cách AH từ những tam giác vuông đồng dạng, tiếp theo đó tính những cạnh của tam giác ABC. Giải: ∆AHB ∽ ∆CHA vì (widehatAHB = widehatAHC) = 900, (widehatBAH = widehatACH) (fracAHCH = fracBHCH) => AH2 = CH.BH = 25.36 => AH2 = 900 => AH = 300 Vậy (S_ABC) = (frac12) AH.BC = (frac12).30.(25 + 26) = 915 cm2 Bài 52 trang 85 - Sách giáo khoa toán 8 tập 2 Cho một tam giác vuông, trong số đó có cạnh huyền dài 20cm và một cạnh góc vuông dài 12cm. Tính độ dài hình chiếu cạnh góc vuông kia trên cạnh huyền. Giải: ∆ABC vuông tại A có đường cao AH, BC = 20cm, AB = 12cm. Ta tính HC, ∆ABC ∽ ∆CBA vì Góc B chung, ( widehatA) = ( widehatH) = 900 => (fracAHCB= fracBHBA) => AB2 = HB.CB => BH = (fracAB^2CB= frac12^220) = 7,2 (cm) => CH = BC - BH = 20 - 7,2 = 12,8 Giaibaitap.me Bài 56 trang 92 sgk toán 8 tập 2 Xác định tỉ số của hai đoạn thẳng AB và CD trong những trường hợp sau: a)AB = 5cm, CD = 15 cm; b)AB = 45 dm, CD = 150 cm; c)AB = 5CD. Giải a)AB = 5cm và CD = 15cm =>(AB over CD = 5 over 15 = 1 over 3) b)AB = 45dm = 450cm và CD = 150 cm =>(AB over CD = 450 over 150 = 3) c)AB = 5CD =>(AB over CD = 5) Bài 57 trang 92 sgk toán 8 tập 2 Cho tam giác ABC (AB < AC). Vẽ đường cao AH, đường phân giác AD, đường trung tuyến AM. Có nhận xét gì về vị trí của ba điểm H, D, M. Giải +Nhận xét: D luôn nằm trong tâm H và M. +Chứng minh: AD là đường phân giác của ∆ABC. =>(AB over AC = DB over DC) AB < AC =>DB < DC => DB + DC < DC + DC =>BD + DC < 2DC hay BC < 2DC => DC >(BC over 2) Mà (MC = BC over 2) (M là trung điểm của BC) =>DC > MC =>M nằm trong tâm D và C (1) +Mặt khác: (widehat CAH = 90^0 - hat C) (∆CAH vuông tại H) (hat A + hat B + hat C = 180^0) (tổng 3 góc ∆ABC) =>(widehat CAH = hat A + hat B + hat C over 2 - hat C) =>(widehat CAH = hat A over 2 + hat B over 2 - hat C over 2 = hat A over 2 + hat B - hat C over 2) Vì AB < AC =>(widehat C < widehat B Rightarrow widehat B - widehat C > 0) Do đó: (widehat CAH > hat A over 2) hay (widehat CAH > widehat CAD) =>Tia AD nằm trong tâm hai tia AH và AC =>D nằm trong tâm hai điểm H và C (2) Từ (1) và (2) => D nằm trong tâm H và M. Bài 58 trang 92 sgk toán 8 tập 2 Cho tam giác cân ABC (AB = AC), vẽ những đường cao BH, CK (H.66). a)Chứng minh BK = CH. b)Chứng minh KH//BC. c)Cho biết BC = a, AB = AC = b. Tính độ dài đoạn thẳng HK. Hướng dẫn câu c): -Vẽ thêm đường cao AI, xét hai tam giác đồng dạng IAC và HBC rồi tính CH. -Tiếp theo, xét hai tam giác đồng dạng AKH và ABC rồi tính HK. Giải a)Xét hai tam giác vuông BKC và CHB có: (widehat KBC = widehat HCB) (∆ABC cân tại A) BC là cạnh chung =>∆BKC = ∆CHB =>BK = CH b)Ta có : AB = AC (∆ABC cân tại A) BK = CH (∆BKC = ∆CHB) => AK = AH Do đó : (AK over AB = AH over AC) =>KH // BC (định lí Ta lét hòn đảo) c)BH cắt CK tại M =>M là trực tâm của ∆ABC =>AM ⊥ BC tại I. Ta có : ∆AIC ∽ ∆BHC vì (left{ matrixhat I = hat H = 90^0 cr hat Cchung cr right.) =>(IC over HC = AC over BChaya over 2 over HC = b over a = > HC = a^2 over 2b) =>(AH = b - a^2 over 2b = 2b^2 - a^2 over 2b) Mà HK // BC => (HK over BC = AH over AC = > HK = BC.AH over AC) =>(HK = a over bleft( 2b^2 - a^2 over 2b right) = 2ab^2 - a^2 over 2b^2) Bài 59 trang 92 sgk toán 8 tập 2 Hình thang ABCD (AB//CD) có AC và BD cắt nhau tại O, AD và BC cắt nhau tại K. Chứng minh rằng OK trải qua trung điểm của những cạnh AB và CD. Giải Qua O kẻ đường thẳng tuy nhiên tuy nhiên với AB, CD cắt AD, BC lần lượt tại E, F. Ta có: OE = OF (xem cách chứng tỏ ở bài tập 20) Do đó: (AN over EO = KN over KO) (AN // EO) Mà (BN over OF = KN over KO) (BN // OF) =>(AN over EO = BN over FO) Mà OE = OF =>AN = BN hay N là trung điểm của AB. Chứng minh tương tự: (DM over OE = CM over OF = > MD = MC) =>M là trung điểm của CD. Bài 60 trang 92 sgk toán 8 tập 2 Cho tam giác vuông ABC, và đường phân giác BD (D thuộc cạnh AC). a)Tính tỉ số . b)Cho biết độ dài AB = 12,5 cm, hãy tính chu vi và diện tích s quy hoạnh của tam giác ABC. Giải a)Tam giác BCA vuông tại A có nên là một nửa tam giác đều =>(AB over BC = 1 over 2) Vì BD là đường phân giác của ∆ABC nên: (DA over DC = BA over BC) b)∆ABC vuông tại A nên AC2 = BC2 – AB2, BC = 2AB =>AC2 = 4AB2 – AB2 = 3AB2 =>AC=(sqrt 3AB^2 = ABsqrt 3 = 12,5sqrt 3 approx 21,65left( cm right)) Gọi p. là chu vi ∆ABC =>p. = AB + BC + CA =>p. = 3AB + AC = 3.12,5 + 12,5(sqrt 3 ) =>p. = 12,5 (3+(sqrt 3 ) approx 59,15left( cm right)) Và (S_ABC = 1 over 2AB.AC approx 135,31(cm^2)) Bài 61 trang 92 sgk toán 8 tập 2 Tứ giác ABCD có AB = 4cm, BC = 20 cm, CD = 25 cm, DA = 8cm, đường chéo BD = 10cm. a)Nêu cách vẽ tứ giác ABCD có kích thước đã cho ở trên. b)Các tam giác ABD và BDC có đồng dạng với nhau không? Vì sao? c)Chứng minh rằng AB // CD. Giải a)Vẽ ∆DBC biết BD = 10 cm, BC = 20 cm, DC = 25 cm. Trên nửa mặt phẳng bờ BD không chứa C vẽ hai cung tròn tâm B và tâm D bán kính lần lượt là 4 cm và 8 cm. Hai cung này cắt nhau tại A. Vẽ những đoạn BA, DA được tứ giác ABCD. b)Ta có: (AB over BD = 4 over 10 = 2 over 5;BD over DC = 10 over 25 = 2 over 5;AD over BC = 8 over 20 = 2 over 5) =>(AB over BD = BD over DC = AD over BC = > Delta ABDDelta BDC) c)∆ABD∽ ∆BDC =>(widehat ABD = widehat BDC) lại so le trong. =>AB // DC hay ABCD là hình thang. Giaibaitap.me Bài 10 trang 103 sgk toán lớp 8 - tập 2 1.Gấp hình 33a theo những nét đã chỉ ra thì đã có được một hình hộp chữ nhật hay là không? 2. Kí hiệu những đỉnh hình hộp gấp được như hình 33b a) Đường thẳng BF vuông góc với những mặt phẳng nào? b) Hai mặt phẳng (AEHD) và (CGHD) vuông góc với nhau, vì sao? Hướng dẫn: 1. Gấp hình 33a theo những nét đã chỉ ra thì đã có được một hình hộp chữ nhật 2. a) Trong hình hộp ABCD.EFGH thì: BF tuy nhiên tuy nhiên với mp (DHGC) và mp (DHEA). b) Hai mặt phẳng (AEHD) và (CGHD) vuông góc với nhau vì mặt phẳng (AEHD) chứa đường thẳng EH vuông góc với mặt phẳng (CGHD) tại H. Bài 11 trang 104 sgk toán lớp 8 - tập 2 11. a) Tính những kích thước của một hình hộp chữ nhật, biết rằng chúng tỉ lệ với 3, 4, 5 và thể tích của hình hộp này là 480cm3 b) Diện tích toàn phần của một hình lập phương là 486cm2. Thể tích của nó bằng bao nhiêu? Hướng dẫn: Gọi a, b, c là ba kích thước của hình hộp chứ nhật. Vì a, b, c tỉ lệ với 3; 4; 5 nên (fraca3) = (fracb4) = (fracc5) = t ( t > 0) => a = 3t; b = 4t; c = 5t (1) Mà thể tích hình hộp là 480cm3 nên a.b.c = 480 (2) Từ (1) và (2) suy ra 3t.4t.5t = 480 <=> 60t3 = 480 <=> t3 = 8 <=> t = 2 Do đó: a = 6(cm); b = 8(cm); c = 10 (cm) Vậy những kích thước của hình hộp là 6cm; 8cm; 10cm. Bài 12 trang 104 sgk toán lớp 8 - tập 2 12. A, B, C và D là những đỉnh của hình hộp chữ nhật cho ở hình 34. Hãy điền số thích hợp vào những ô trống ở bảng sau: AB 6 13 14 BC 15 16 34 CD 42 70 62 DA 45 75 75 Kết quả bài 12 minh họa công thức quan trọng sau: DA = (sqrtAB^2+BC^2+CD^2) Hướng dẫn: Trước hết ta chứng tỏ hệ thức sau: DA2 = AB2 + BC2 + CD2 Ta có : ∆ABC vuông tại C => BD2 = DC2 + BC2 ∆ABD vuông tại B => AD2 = BD2 + AB2 AD2 = DC2 +BD2 + AB2 Áp dụng hệ thức này ta sẽ tính được độ dài một cạnh lúc biết ba độ dài kia do đó ta có: AB 6 13 14 25 BC 15 16 23 34 CD 42 40 70 62 DA 45 45 75 75 Bài 13 trang 104 sgk toán lớp 8 - tập 2 a) Viết công thức tính thể tích của hình hộp chữ nhật ABCD.MNPQ (h35) b) Điền số thích hợp vào những ô trống ở bảng sau: Chiều dài 22 18 15 20 Chiều rộng 14 Chiều cao 5 6 8 18 Diện tích một đáy 90 260 Thể tích 1320 2080 Hướng dẫn: VABCD.MNPQ = MN. NP. NB b) Điền vào chỗ trống: 1) 2) 3) 4) Chiều dài 22 18 15 20 Chiều rộng 14 5 11 13 Chiều cao 5 6 8 18 Diện tích một đáy 308 90 165 260 Thể tích 1540 540 1320 2080 1) Diện tích 1 đáy: 22 x 14 = 308 Thể tích: 22x 14 x 5 = 1540 2) Chiều rộng: 90 : 18 = 5 Thể tích: 18 x 5 x 6 = 90 x 6 = 540 3) Chiều rộng: 1320 : (15 x 8) = 11 Diện tích 1 đáy: 15 x 11 = 165 4) Chiều rộng: 260 : 20 = 13 Chiều cao: 2080 : 260 = 18 Bài 14 trang 104 sgk toán lớp 8 - tập 2 14. Một bể nước hình hộp chữ nhật có chiều dài 2m. Lúc đầu bể không còn nước. Sau khi đổ vào bể 120 thùng nước, mỗi thùng chứa 20 lít thì mực nước của bể là 0,8m. a) Tính chiều rộng của bể nước. b) Người ta đổ thêm vào bể 60 thùng nước nữa thì đầy bể. Hỏi bể cao bao nhiêu mét? Hướng dẫn: a) Thể tích nước đổ vào: 120 x 20 = 2400 (l ) = 2,4m3 Chiều rộng của bể nước: 2,4 : (2 x 0,8) = 1,5 (m) b) Thể tích của hồ nước: 2400 + 60 x 20 = 3600 (l) = 3,6m3 Chiều cao của hồ nước: 3,6 : (2 x 1,5) = 1,2m. Giaibaitap.me
Page 10









Page 13
Page 14
Page 15
Page 16
Page 17



Page 19







Page 22




Page 24
Page 25





Share Link Download Giải toán lớp 8 trang 40 miễn phí
Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Giải toán lớp 8 trang 40 tiên tiến và phát triển nhất và Chia Sẻ Link Cập nhật Giải toán lớp 8 trang 40 miễn phí.
Giải đáp vướng mắc về Giải toán lớp 8 trang 40
Nếu sau khi đọc nội dung bài viết Giải toán lớp 8 trang 40 vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha
#Giải #toán #lớp #trang
