Thủ Thuật Hướng dẫn Giải bất phương trình mũ bằng phương pháp đặt an phụ không hoàn toàn Mới Nhất
Bạn đang tìm kiếm từ khóa Giải bất phương trình mũ bằng phương pháp đặt an phụ không hoàn toàn được Update vào lúc : 2022-05-19 21:45:07 . Với phương châm chia sẻ Kinh Nghiệm về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Cập nhật lúc: 15:04 21-08-2015 Mục tin: LỚP 12
>> Luyện thi TN THPT & ĐH năm 2022 trên trang trực tuyến Tuyensinh247.com. Học mọi lúc, mọi nơi với Thầy Cô giáo giỏi, khá đầy đủ những khoá: Nền tảng lớp 12; Luyện thi nâng cao; Luyện đề đủ dạng; Tổng ôn tinh lọc.








09:04:5318/12/2022
Các em đã ôn tập về luỹ thừa trong bài hướng dẫn trước, trong phần này toàn bộ chúng ta sẽ ôn lại kiến thức và kỹ năng về phương trình mũ và bất phương trình mũ. Nếu những em chưa nhớ những tính chất của hàm số mũ, những em hoàn toàn có thể xem lại Tại Đây
A. PHƯƠNG TRÌNH MŨ
I. Phương trình mũ cơ bản
+ Là dạng phương trình ax = b; (*), với a, b cho trước và 0 - Nếu b≤ 0: Phương trình (*) vô nghiệm - Nếu b>0: II. Phương pháp giải Phương trình mũ và Bất phương trình mũ 1. Phương pháp đưa về cùng cơ số - Ta sử dụng phép biến hóa tương tự sau: af(x) = ag(x) ⇔ a = 1 hoặc - Logorit hoá và đưa về cùng cơ số: * Dạng 1: Phương trình af(x) = b ⇔ * Dạng 2: Phương trình: af(x) = bg(x) ⇔ hoặc: * Ví dụ: Giải những phương trình sau: a) b) * Lời giải: a) ⇔ ⇔ x2 - x + 8 = 2 - 6x ⇔ x2 + 5x + 6 = 0 ⇔ x= -2 hoặc x = -3 b) ⇔ ⇔ ⇔ ⇔ x = 1 2. Phương pháp dùng ẩn phụ * Khi sử dụng phương pháp này ta nên thực thi theo tiến trình sau: B1: Đưa PT, BPT về dạng ẩn phụ quen thuộc. B2: Đặt ẩn phụ thích hợp và tìm Đk cho ẩn phụ. B3: Giải PT, BPT với ẩn phụ mới và tìm nghiệm thỏa Đk. B4: Thay giá trị t tìm kiếm được vào giải PT, BPT mũ cơ bản B5: Kết luận. * Loại 1: Các số hạng trong PT, BPT hoàn toàn có thể màn biểu diễn qua af(x) nên được đặt t = af(x). - Hay gặp một số trong những dạng sau: + Dạng 1: Aa2f(x) + Baf(x) + C = 0 ⇒ bậc 2 ẩn t. + Dạng 2: Aa3f(x) + Ba2f(x) + Caf(x) + D = 0 ⇒ bậc 3 ẩn t. + Dạng 3: Aa4f(x) + Ba2f(x) + C = 0 ⇒ trùng phương ẩn t. > Lưu ý: Trong loại này ta còn gặp một số trong những bài mà sau khi để ẩn phụ ta thu được một phương trình, Bpt vẫn chứa x ta gọi đó là những bài toán đặt ẩn phụ không hoàn toàn. * Loại 2: Phương trình đẳng cấp và sang trọng bậc n riêng với af(x) và bf(x). - Hay gặp một số trong những dạng sau: + Dạng 1: Aa2f(x) + B(a.b)f(x) + Cb2f(x) = 0 ⇒ Chia 2 vế cho a2f(x) đưa về loại 1 dạng 1 + Dạng 2: Aa3f(x) + B(a2.b)f(x) + C(a.b2)f(x) + D.b3f(x) = 0 ⇒ Chia 2 vế cho a3f(x) đưa về loại 1 dạng 2 º Tổng quát: Với dạng này ta sẽ chia cả hai vế của Pt cho an.f(x) hoặc bn.f(x) với n là số tự nhiên lớn số 1 có trong Pt Sau khi chia ta sẽ đưa được Pt về loại 1. Loại 3: Trong phương trình có chứa 2 cơ số nghịch hòn đảo + Dạng 1: A.af(x) + B.bf(x) + C = 0 với a.b=1 ⇒ Đặt ẩn phụ t = af(x) ⇒ bf(x) = 1/t + Dạng 2: A.af(x) + B.bf(x) + C.cf(x) = 0 với a.b=c2. ⇒ Chia 2 vế của Pt cho cf(x) và đưa về dạng 1. 3. Phương pháp logarit hóa + Đôi khi ta không thể giải một PT, BPT mũ bằng phương pháp đưa về cùng một cơ số hay dùng ấn phụ được, khi đó ta thể lấy logarit hai vế theo cùng một sơ số thích hợp nào đó PT, BPT mũ cơ bản (phương pháp này gọi là logarit hóa) + Dấu hiệu nhận ra: PT loại này thường có dạng af(x).bg(x).ch(x)=d (tức là trong phương trình có chứa nhiều cơ số rất khác nhau và số mũ cũng rất khác nhau) khi đó ta hoàn toàn có thể lấy logarit 2 vế theo cơ số a (hoặc b, hoặc c). B. BẤT PHƯƠNG TRÌNH MŨ 1. Bất phương trình mũ cơ bản - Xét bất phương trình ax > b - Nếu b≤0, tập nghiệm của bất PT là R vì ax > 0 với mọi x∈R - Nếu b>0, thì BPT tương tự với ax > - Nếu a > 1 thì nghiệm của bất PT là x > logab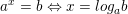 (0
(0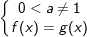
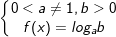
 ⇔
⇔ 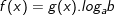
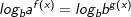 ⇔
⇔ 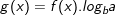
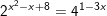
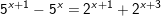
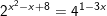
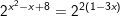
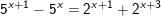
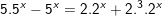

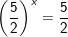

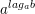
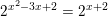 d)
d) 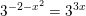
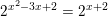 ⇔ x2 - 3x + 2 = x+2 ⇔ x2 - 3x - x + 2 - 2 = 0
⇔ x2 - 3x + 2 = x+2 ⇔ x2 - 3x - x + 2 - 2 = 0
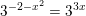 ⇔ -2 - x2 = 3x ⇔ x2 + 3x + 2 =0 ⇔ x=-1 hoặc x = -2
⇔ -2 - x2 = 3x ⇔ x2 + 3x + 2 =0 ⇔ x=-1 hoặc x = -2 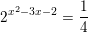 b)
b) 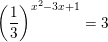 c) 2x+1 + 2x-2 = 36
c) 2x+1 + 2x-2 = 36 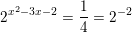 ⇔ x2 - 3x - 2 = -2 ⇔ x2 - 3x = 0 ⇔ x = 0 hoặc x = 3
⇔ x2 - 3x - 2 = -2 ⇔ x2 - 3x = 0 ⇔ x = 0 hoặc x = 3 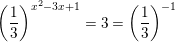 ⇔ x2 - 3x + 1 = -1 ⇔ x2 - 3x + 2 = 0 ⇔ x = 1 hoặc x = 2
⇔ x2 - 3x + 1 = -1 ⇔ x2 - 3x + 2 = 0 ⇔ x = 1 hoặc x = 2 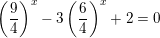 ⇔
⇔ 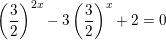 đặt t = (3/2)x với t>0 ta được phương trình
đặt t = (3/2)x với t>0 ta được phương trình 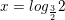
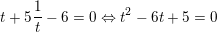 ⇔ t =1 hoặc t =5 (thoả Đk t>0)
⇔ t =1 hoặc t =5 (thoả Đk t>0) 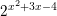 > 4x-1 d) 271-2x <
> 4x-1 d) 271-2x < 
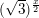 >
> 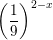 f)
f) 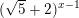 ≥
≥ 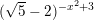
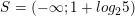
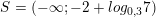
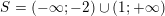
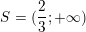
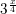 >
> 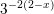 ⇔
⇔ 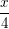 > -2(2-x)
> -2(2-x) 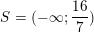
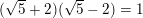
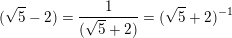
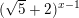 ≥
≥  ⇔
⇔ 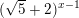 ≥
≥ 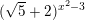
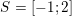
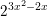 > 32
> 32 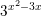 > 3-2
> 3-2  Reply
Reply
 4
4
 0
0
 Chia sẻ
Chia sẻ
