Kinh Nghiệm Hướng dẫn Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện đều Mới Nhất
Pro đang tìm kiếm từ khóa Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện đều được Cập Nhật vào lúc : 2022-05-01 15:58:13 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tìm hiểu thêm tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha.Mặt cầu ngoại tiếp tứ diện là dạng bài tập rất hay gặp trong những đề ôn thi ĐH. Để hoàn toàn có thể ôn luyện thật hiệu suất cao và đạt được điểm trên cao, những bạn học viên hãy cùng theo dõi nội dung bài viết dưới đây, sẽ có được khá đầy đủ lý thuyết và công thức tính bán kính mặt cầu ngoại tiếp tứ diện cho học viên tìm hiểu thêm.
Nội dung chính- 2. Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện
- 3. Công thức tính bán kính mặt cầu ngoại tiếp hình chóp
- 3.1. Dạng 1: Hình chóp đều
- 3.2. Dạng 2: Hình chóp có cạnh bên vuông góc với mặt đáy
- 3.3. Dạng 3: Hình chóp xuất hiện bên vuông góc với đáy
- 4. Một số bài tập tính bán kính mặt cầu ngoại tiếp tứ diện
- Mặt cầu ngoại tiếp khối đa diện là gì?
- Lý thuyết cơ bản của mặt cầu ngoại tiếp khối đa diện:
- Các dạng mặt cầu ngoại tiếp khối đa diện:
- Công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện
- Bài tập có lời giải về mặt cầu ngoại tiếp khối đa diện
Mặt cầu ngoại tiếp tứ diện là mặt cầu trải qua 4 đỉnh hay 4 điểm A, B, C, D. Để tìm và xác lập được tọa độ tâm và bán kính mặt cầu ngoại tiếp tứ diện, toàn bộ chúng ta tuân theo 3 cách sau:
Cách 1: Sử dụng tính chất IA = IB = IC = ID. Gọi I là tâm mặt cầu => tọa độ tâm và bán kính mặt cầu.
Cách 2: Ví dụ phương trình mặt cầu là $x^2+y^2+z^2+2ax+2by+2cz+d=0$.
Vì mặt cầu cùng trải qua 4 điểm A, B, C, D nên tọa độ sẽ thỏa mãn nhu cầu phương trình mặt cầu. Ta sẽ có được hệ 4 phương trình ẩn a, b, c, d. Giải hệ này ta sẽ nhận được phương trình mặt cầu => tọa độ tâm và bán kính mặt cầu.
Cách 3: Ta viết phương trình mặt phẳng trung trực của AB, CD, BC. Giao của ba mặt phẳng này là tâm mặt cầu ngoại tiếp tứ diện ABCD hay tâm mặt cầu trải qua 4 điểm A, B, C, D.
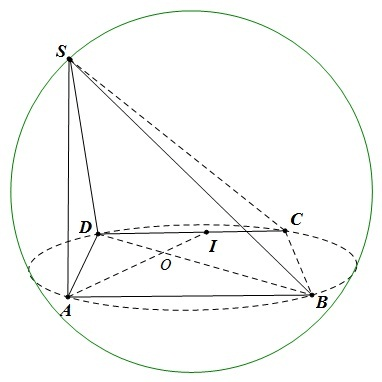
2. Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện
Phương pháp chung để tính nhanh công thức mặt cầu ngoại tiếp tứ diện là:
-
Chúng ta xác lập tâm của đáy để từ đó dựng được đường thẳng d vuông góc với mặt đáy.
-
Dựng mặt phẳng trung trực (P) của một cạnh bên bất kì.
-
Tâm mặt cầu là giao điểm của d và (P).
3. Công thức tính bán kính mặt cầu ngoại tiếp hình chóp
Bài toán tính bán kính mặt cầu ngoại tiếp hình chóp là dạng bài tập rất phổ cập. Ta có những dạng công thức dưới đây:
3.1. Dạng 1: Hình chóp đều
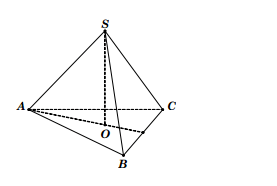
Ta có a là độ dài cạnh bên của hình chóp, h là độ cao của hình chóp.
R = $fraca^22h$
Ví dụ: Tính bán kính mặt cầu ngoại tiếp khối chóp đã cho biết thêm thêm ta có hình chóp tứ giác đều S.ABCD có cạnh đáy bằng a, cạnh bên bằng 3a.
Giải:
Gọi O đó đó là tâm hình vuông vắn ABCD, vậy ta có SO$perp $(ABCD).
ao = $fracAC2=fracasqrt22$
Ta xét tam giác SAO vuông tại O.
SO = $sqrtSA^2-AO^2=fracasqrt342$
Ta lại sở hữu R = $fracSA^22SO=frac9asqrt3434$
3.2. Dạng 2: Hình chóp có cạnh bên vuông góc với mặt đáy
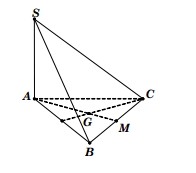
Ta gọi r, h là bán kính và độ cao đường tròn ngoại tiếp đa giác đáy. Có:
R=$sqrt(frach2)^2+r^2$
Ví dụ: Hãy tính bán kính R mặt cầu ngoại tiếp tứ diện OABC khi cho tứ diện OABC, những cạnh OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = 2a, OC = 2a.
Giải:
Ta có tam giác OBC vuông tại O nên h = OA = a
Ta có BC =$sqrtOB^2+OC^2=2sqrt2a$
r = $asqrt2$
Theo công thức ta vận dụng:
R = $sqrt(fraca2)^2+(asqrt2)^2=frac3a2$
3.3. Dạng 3: Hình chóp xuất hiện bên vuông góc với đáy
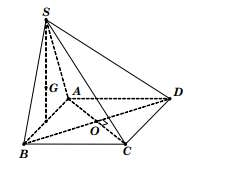
Bán kính đường tròn ngoại tiếp mặt bên và mặt đáy được gọi lần lượt là $R_b,R_d$. GT là độ dài giao tuyến mặt bên và đáy.
R=$sqrtR_b^2+R_d^2-fracGT^24$
Ví dụ: Hãy tính bán kính mặt cầu ngoại tiếp hình chóp S.ABCD, biết hình chóp S.ABCD có đáy ABCD là hình vuông vắn có cạnh a. Tam giác SAB đều, nằm trong mặt phẳng vuông góc với đáy.
Giải
Giao tuyến của (SAB) và (ABCD) là AB.
Bán kính đường tròn ngoại tiếp đáy $R_d=AO=fracasqrt22$
Bán kính R đường tròn ngoại tiếp mặt bên là R = SG =$fracasqrt33$
Ta có công thức:
$R=sqrtR_b^2+R_d^2-fracGT^24=fracasqrt216$
4. Một số bài tập tính bán kính mặt cầu ngoại tiếp tứ diện
Bài 1: Hãy tính bán kính R của mặt cầu ngoại tiếp hình chóp S.ABCD biết rằng S.ABCD có đáy là hình chữ nhật. BC = 4a, AB = 3a, SA = 12a và SA vuông góc với đáy.
Giải:
Ta có $R_d=fracAC2=fracsqrtAB^2+BC^22=frac5a2$
=> R=$sqrtR_d^2+(frach2)^2=sqrt(frac5a2)^2+(frac12a2)^2=frac13a2$
Bài 2: Cho hình chóp S.ABC có những cạnh SA, SB, SC bằng nhau và đều bằng a. Hãy tính diện tích s quy hoạnh S mặt cầu ngoại tiếp hình chóp biết rằng $widehatASC=widehatASB=90^circ$
Giải:
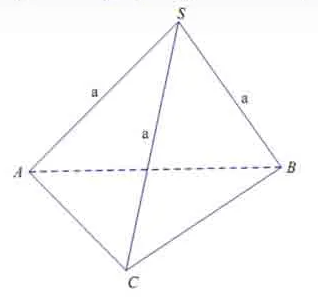
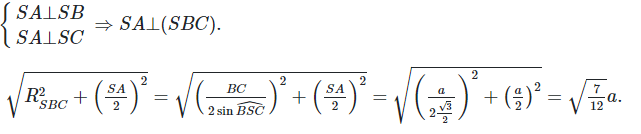
S = $4pi R^2=frac7pi a^23$
Bài 3: Tính bán kính R mặt cầu ngoại tiếp hình chóp khi cho hình chóp S.ABC có đáy ABC là tam giác cân tại A, cạnh bên SA = 2a và vuông góc với đáy (ABC). AB = a và $widehatBAC=120^circ$
Giải:
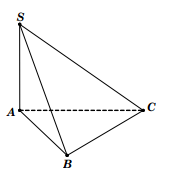
Áp dụng định lý cos ta có:
BC =$sqrtAB^2+AC^2-2AB.AC.coswidehatBAC=asqrt3$
Lại có r = $fracAB.BC.AC4.S_ABC=fracAB.BC.AC2.AB.AC.sinwidehatBAC=a$
R=$sqrt(frach2)^2+r^2=sqrt(frac2aa)^2+a^2=asqrt2$
Bài 4: Cho hình chóp S.ABCD, đáy ABCD là một hình vuông vắn. Tính bán kính mặt cầu ngoại tiếp hình chóp biết SA vuông góc với mặt phẳng (ABCD) và SC = 2a.
Giải:
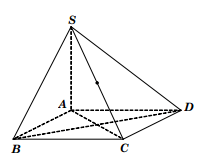
Ta có:
R = $fracAC2$, h = SA
R = $sqrt(fracAC2)^2+(fracSA2)^2=frac12S_c=a$
Bài 5: Hình chóp S.ABC có đáy là tam giác vuông ABC, vuông tại C. Tính bán kính mặt cầu ngoại tiếp hình chóp biết mặt phẳng (SAB) vuông góc với đáy, SA = SB = a và $widehatASB=120^circ$
Giải:
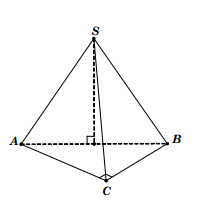
AB = $sqrtSA^2+SB^2-2SA.SB.coswidehatASB=asqrt3$
=> GT=AB=$asqrt3$
$R_d=fracAB2=fracasqrt33$
$R_b=fracSA.SB.AB4.S_ABC=fracSA.SB.AB2.SA.SB.sin120^circ=a$
Trên đấy là toàn bộ lý thuyết và cách giải rõ ràng nhất của bài toán mặt cầu ngoại tiếp tứ diện. Để hoàn toàn có thể đạt được kết quả cao thì hãy phối hợp rèn luyện thêm nhiều dạng bài khác nữa. Các bạn hoàn toàn có thể truy vấn nền tảng Vuihoc.vn và Đk thông tin tài khoản để luyện đề ôn thi THPT Quốc gia!
>> Xem thêm: Toán 12: Lý thuyết phương trình mặt cầu và những dạng bài tập
Mặt cầu ngoại tiếp khối đa diện là gì? Công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện? Và những bài tập có lời giải giúp bạn hiểu cặn kẽ hơn về mặt cầu ngoại tiếp khối đa diện.
Xem thêm:
Mặt cầu ngoại tiếp khối đa diện là gì?
Mặt cầu ngoại tiếp khối đa diện là hình cầu trải qua mọi đỉnh của khối đa diện.
Lý thuyết cơ bản của mặt cầu ngoại tiếp khối đa diện:
- Bán kính mặt cầu ngoại tiếp : R
- Diện tích mặt cầu ngoại tiếp: S=4.π.R2
- Thể tích mặt cầu ngoại tiếp: V = (4.π.R3)/3
Các dạng mặt cầu ngoại tiếp khối đa diện:
- Mặt cầu ngoại tiếp khối đa diện có cạnh bên vuông góc với đáy
- Mặt cầu ngoại tiếp khối đa diện hình chóp đều
- Mặt cầu đa diện xuất hiện bên vuông góc với đáy
Công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện
Mặt cầu ngoại tiếp quan trọng là toàn bộ chúng ta cần xác lập được bán kính(R).
Với mỗi dạng mặt cầu ngoại tiếp khối đa diện sẽ có được phương pháp tính bán kính riêng. Sau đấy là phương pháp tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện.
Dạng 1: Khối đa diện có cạnh bên vuông góc đáy.
Công thức:


Trong số đó:
- R là bán kính khối cầu ngoại tiếp
- h là độ cao
- r là bán kính đường tròn ngoại tiếp đáy

Dạng 2: Khối đa diện chóp đều hoặc những cạnh bên bằng nhau

Trong số đó:
- R là bán kính khối cầu ngoại tiếp
- h là độ cao
- b là độ dài cạnh bên
Dạng 3: Mặt cầu đa diện xuất hiện bên vuông góc với đáy


Trong số đó:
- a là cạnh huyền vuông góc với đáy
- R là bán kính đường tròn ngoại tiếp
Bài tập có lời giải về mặt cầu ngoại tiếp khối đa diện
Bài 1: Cho hình chóp S.ABCD có đáy ABCD là hình vuông vắn tại A, SA vương góc với mặt phẳng (ABCD) và SC=4a. Tính bán kính mặt cầu ngoại tiếp hình chóp.
Đáp án:
 S.ABCD
S.ABCD Ta có : BC⊥AB và BC⊥SA ⇒ BC⊥(SAB) ⇒ BC⊥SB
Tương tự ta cũng chứng tỏ được: CD ⊥ SD
Ta có: SA ⊥ (ABCD) ⇒ SA ⊥ AC
Ba điểm A, B, D cùng nhìn SC dưới một góc vuông.
Như vậy, bán kính mặt cầu S.ABCD là R=SC/2=4a/2=2a
Bài 2: Cho hình chóp S.ABCD có đáy là hình vuông vắn cạnh a, SAD là tam giác đều và nằm trong mặt phẳng vuông góc với đáy. Gọi E và F lần lượt là trung điểm của BC và CD. Tính bán kính R của khối cầu ngoại tiếp hình chóp S.CEF. Chọn đáp án đúng.
A. R= (a√29)/8
B. R=(5a√3)/12
C. R=(a√37)/6
D. R=(a√93)/12
Lời giải:

Gọi H là trung điểm của AD ➝ SH ⊥ (ABCD)
Ta thấy tâm I nằm trên trục d trải qua trung điêm O của EF và ⊥(ABCD), I, S cùng phía với mặt phẳng ABCD.
Ta có:

∆HFO vuông tại N ta có:

Ta có: OC2 + OI2 = R2 = IK2 + KS2
Đặt OI = x ta có:

Như vậy ta có:

Đáp án: D
Trên đấy là nội dung về mặt cầu ngoại tiếp và công thức tính nhanh bán kính mặt cầu ngoại tiếp khối đa diện. Hy vọng những kiến thức và kỹ năng Góc Hạnh Phúc mang lại giúp bạn làm rõ hơn về mặt cầu ngoại tiếp.
 Reply
Reply
 3
3
 0
0
 Chia sẻ
Chia sẻ
Chia Sẻ Link Tải Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện đều miễn phí
Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Clip Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện đều tiên tiến và phát triển nhất và Chia Sẻ Link Cập nhật Công thức tính nhanh bán kính mặt cầu ngoại tiếp tứ diện đều Free.