Cách góp nghiệm bất phương trình Đầy đủ

Thủ Thuật Hướng dẫn Cách góp nghiệm bất phương trình Chi Tiết

Bạn đang tìm kiếm từ khóa Cách góp nghiệm bất phương trình được Cập Nhật vào lúc : 2022-05-01 10:50:11 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha.

VnHocTap.com trình làng đến những em học viên lớp 12 nội dung bài viết Phương pháp giải bất phương trình mũ và logarit, nhằm mục đích giúp những em học tốt chương trình Toán 12.

Nội dung nội dung bài viết Phương pháp giải bất phương trình mũ và logarit: PHƯƠNG PHÁP GIẢI BẤT PHƯƠNG TRÌNH MŨ VÀ LOAGRIT I. PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG CHO BPT MŨ. Phương pháp: Ta hoàn toàn có thể trình diễn theo hai cách sau: Cách 1: Bất phương trình được biến hóa về dạng. Vậy tập nghiệm của bất phương trình. Cách 2: Bất phương trình được biến hóa về dạng. Vậy tập nghiệm của bất phương trình. Nhận xét: Như vậy, để thực thi bài toán trên ở cả hai cách toàn bộ chúng ta đều thực thi một việc làm là đưa bất phương trình về dạng có cùng cơ số, tuy nhiên: Trong cách 1, với việc sử dụng cơ số a1 nên dấu bất đẳng thức không đổi chiều. Trong những trường hợp tương tự những em học hãy lựa chọn theo phía này. Nhận xét: Như vậy, để thực thi bài toán trên ở cả hai cách toàn bộ chúng ta đều thực thi một việc làm là đưa bất phương trình về dạng có cùng cơ số, tuy nhiên: Trong cách 1, toàn bộ chúng ta đã tìm cách biến hóa theo và ở đây những em học viên cũng cần phải lưu ý rằng cơ số này nhỏ hơn 1. Trong cách 2, toàn bộ chúng ta đã sử dụng ý tưởng về cơ số trung gian đã biết trong phần phương trình mũ. II. PHƯƠNG PHÁP BIẾN ĐỔI TƯƠNG ĐƯƠNG CHO BẤT PHƯƠNG TRÌNH LOGARIT. Phương pháp: Dạng 1: Với bất phương trình. Dạng 2: Với bất phương trình Dạng 3: Với bất phương trình. 2. Bài toán minh họa: Giải những bất phương trình sau. Ta hoàn toàn có thể trình diễn theo hai cách sau. Biến đổi bất phương trình về dạng. Kết phù thích hợp với Đk ta nhận được tập nghiệm của bất phương trình là (1; 4). Cách 2: Bất phương trình biến hóa tương tự về dạng. Vậy tập nghiệm của bất phương trình là (1; 4). Yêu cầu: Các em học viên hãy so sánh hai cách giải trên và hãy vấn đáp vướng mắc “Có thể sử dụng cách 2 cho bất phương trình trong câu 2 hay là không ?”. Phương pháp: Các dạng đặt ẩn phụ trong trường hợp này cũng tương tự phương trình mũ và phương trình logarit. 2. Bài toán minh họa

Bài toán 1: Giải những bất phương trình sau: Phương trình được biến hóa về dạng chia hai vế bất phương trình. Khi đó, bất phương trình có dạng. Vậy, nghiệm của bất phương trình là [-1; 1]. Nhận xét: Như vậy, thông qua thí dụ trên toàn bộ chúng ta đã được làm quen với ba dạng đặt ẩn phụ cơ bản đã được biết trong phần phương trình mũ. Và ở đây: Với câu toàn bộ chúng ta cần tới phép biến hóa để khuynh hướng cho ẩn phụ t. Và với Đk t > 0 nên kết quả t 0 toàn bộ chúng ta vô hiệu luôn mẫu số sau phép quy đồng. Với câu 3 toàn bộ chúng ta cần sử dụng một vài phép biến hóa đại số để nhận dạng được loại ẩn phụ cho bất phương trình. Và ở đó việc chia cả hai vế của bất phương trình cho một số trong những dương nên dấu bất đẳng thức không đổi chiều.

A. 10

B. 9

C. 8

D. 11

Lời giải

Chọn C

Điều kiện: x > 0

Phương trình

Đặt

thì phương trình trở thành:

Do đó

Số những nghiệm nguyên của bất phương trình là 8.

Bài tập 2. Xét bất phương trình . Tìm toàn bộ những giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng chừng .

A. m ∈ (0; +∞)

B.

C.

D. m ∈ (–∞; 0)

Lời giải

Chọn C

Điều kiện: x > 0

⇔ (1 + log2 x)2 – 2(m + 1) log2 x – 2 < 0  (1)

Đặt t = log2 x .Vì x ∈

nên . Do đó t ∈

(1) thành (1 + t)2 – 2(m + 1) t – 2 < 0 ⇔ t2 – 2mt – 1 <0  (2)

Cách 1: Yêu cầu bài toán tương tự tìm m để bpt (2) có nghiệm thuộc

Xét bất phương trình (2) có: ∆’ = mét vuông + 1 > 0, ∀ m ∈ ℝ

f(t) = t2 – 2mt – 1 = 0 có ac < 0 nên (2) luôn có 2 nghiệm phân biệt t1 < 0 < t2

Khi đó cần

Cách 2: t2 – 2mt – 1 < 0

Khảo sát hàm số f(t) trong (0; +∞) ta được

Bài tập 3. Cho bất phương trình: 9x + (m – 1)․3x + m > 0 (1). Tìm toàn bộ những giá trị của tham số m để bất phương trình (1) nghiệm đúng ∀ x > 1 .

A.

B.

C.

D.

Lời giải

Chọn A

Đặt t = 3x

Vì x > 1 ⇒ t > 3 Bất phương trình đã cho thành: t2 + (m – 1)․t + m > 0 nghiệm đúng ∀ t ≥ 3

nghiệm đúng ∀ t > 3

Xét hàm số

Hàm số đồng biến trên [3; +∞) và

Yêu cầu bài toán tương

Bài tập 4. Có bao nhiêu giá trị nguyên của tham số m ∈ [0; 10] để tập nghiệm của bất phương trình chứa khoảng chừng (256; +∞)

A. 7

B. 10

C. 8

D. 9

Lời giải

Chọn C

Điều kiện:

Với Đk trên bất phương trình trở thành H95

Đặt t = log2 x thì t > 8 vì x ∈ (256; +∞)

Đặt

Yêu cầu bài toán

Xét hàm số

trên khoảng chừng (8; +∞)

Ta có

⇒ f(t) luôn nghịch biến trên khoảng chừng (8; +∞)

Do đó

Mà m ∈ [0; 10] nên m ∈ 3; 4; …; 10.

Vậy có 8 giá trị nguyên của tham số m thỏa mãn nhu cầu yêu cầu bài toán.

Bài tập 5. Tìm toàn bộ những giá trị thực của tham số m để bất phương trình log2 (5x – 1)․log2 (2.5x – 2) ≥ m có nghiệm với mọi x ≥ 1.

A m ≥ 6

B m > 6

C m ≤ 6

D m < 6

Lời giải

Chọn C.

Điều kiện của bất phương trình: x > 0

Ta có log2 (5x – 1)․log2 (2.5x – 2) ≥ m ⇔ log2 (5x – 1)․[1+ log2 (5x – 1)] ≥ m (1)

Đặt t = log2 (5x – 1), với x ≥ 1 ta có t ≥ 2. Khi đó (1) trở thành m ≤ t2 + t (2)

Xét hàm số f(t) = t2 + t trên [2; +∞) ta có f’(t) = 2t + 1 > 0, ∀ t ∈ [2; +∞).

Do đó để bất phương trình đã cho có nghiệm với mọi t ≥ 2 thì

hay m ≤ 6.Bài tập 6. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình có nghiệm?

A. 6

B. 4

C. 9

D. 1

Lời giải

Chọn D.

Điều kiện x2 – 3x + m ≥ 0 (*)

Do m nguyên dương nên m = 1 thỏa mãn nhu cầu (*).

Bài tập 7. Bất phương trình có bao nhiêu nghiệm nguyên dương nhỏ hơn 10.

A. 7

B. 8

C. 9

D. 6

Lời giải

Chọn A

Điều kiện của bất phương trình là x > 0.

Khi đó:

Đặt t = log2 x. Ta có:

Trả lại ẩn ta có

.

Kết phù thích hợp với Đk x > 0 ta có

hoặc hoặc x > 2

Khi đó bất phương trình có 7 nghiệm nguyên dương nhỏ hơn 10.

Bài tập 8. Tìm toàn bộ những giá trị thực của tham số m sao cho bất phương trình m․4x + (m – 1)․2x+2 + m – 1 > 0 nghiệm đúng ∀ x ∈ ℝ?

A. m ≤ 3

B. m ≥ 1

C. –1 ≤ m ≤ 4

D. m ≥ 0

Lời giải

Chọn B.

Bất phương trình ⇔ m․4x + 4(m – 1)․2x + m – 1 > 0 ⇔ m(4x + 4․2x + 1) > 1 + 4․2x

⇔

Đặt 2x = t (t > 0). Khi đó

.

Để bất phương trình ban đầu nghiệm đúng ∀ x ∈ ℝ thì bất phương trình

nghiệm đúng ∀ t > 0.

Đặt

Hàm số nghịch biến trên (0; +∞). Khi đó

, ∀ t > 0 khi và chỉ khi m ≥ f (0) = 1Bài tập 9. Tìm toàn bộ những giá trị của tham số m bất phương trình 4x–1 – m(2x + 1) > 0 có nghiệm ∀ x ∈ ℝ

A. m ∈ (–∞; 0]

B. m ∈ (0; +∞)

C. m ∈ (0; 1)

D. m ∈ (–∞; 0) ∪ (1; +∞)

Lời giải

Chọn A

Ta có:

Đặt 2x = t (t > 0). Yêu cầu bài toán tương tự với

, ∀ t ∈ (0; +∞)

Đặt

Bảng biến thiên

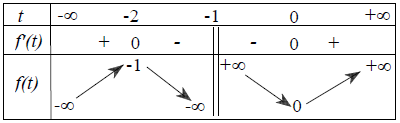
Dựa vào bảng biến thiên có m ≤ 0.

Bài tập 10. Xét bất phương trình . Tìm toàn bộ những giá trị của tham số m để bất phương trình có nghiệm thuộc khoảng chừng .

A. m ∈ (0; +∞)

B.

C.

D. m ∈ (–∞; 0)

Lời giải

Chọn C

Điều kiện: x > 0

⇔ (1 + log2 x)2 – 2(m – 1) log2 x – 2 < 0  (1)

Đặt t = log2 x. Vì

nên . Do đó t ∈

(1) thành (1 + t)2 – 2(m + 1) t – 2 < 0 ⇔ t2 – 2mt – 1 < 0  (2)

Cách 1: Yêu cầu bài toán tương tự tìm m để bpt (2) có nghiệm thuộc

Xét bất phương trình (2) có: ∆’ = mét vuông + 1 > 0, ∀ m ∈ ℝ

f(t) = t2 – 2mt – 1 = 0 có ac < 0 nên (2) luôn có 2 nghiệm phân biệt t1 < 0 < t2

Khi đó cần

Cách 2: t2 – 2mt – 1 < 0

Khảo sát hàm số f(t) trong (0; +∞) ta được

Bài tập 11. Tìm giá trị gần đúng tổng những nghiệm của bất phương trình sau:

A. 12,3

B. 12

C. 12,1

D. 12,2

Lời giải

Chọn C

Điều kiện: 0 < x ≠ 1.

Ta có 24x6 – 2x5 + 27x4 – 2x3 + 1997x2 + 2022

= (x3 – x2)2 + (x3 – 1)2 + 22x6 + 26x4 +1997x2 + 2015 > 0, ∀x

Do đó bất phương trình đã cho tương tự với

Đặt

, ta có bất phương trình

Đặt

. Ta có

Dấu bằng xẩy ra khi

Bài tập 12. Tìm toàn bộ giá trị thực của tham số m để bất phương trình 4x – m․2x+1 + 3 – 2m ≤ 0 có nghiệm thực.

A. m ≥ 2

B. m ≤ 3

C. m ≤ 5

D. m ≥ 1

Lời giải

Chọn D

Ta có 4x – m․2x+1 + 3 – 2m ≤ 0 ⇔ (2x)2 – 2m․2x + 3 – 2m ≤ 0

Đặt 2x = t (t > 0)

Ta có bất phương trình tương tự với

Xét

trên (0; +∞)

Bảng biến thiên

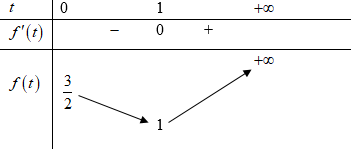
Vậy để bất phương trình có nghiệm thực thì m ≥ 1.

Bài tập 13. Tìm toàn bộ những giá trị thực của tham số m để bất phương trình nghiệm đúng với mọi giá trị x ∈ (1; 64).

A. m ≤ 0

B. m ≥ 0

C. m < 0

D. m > 0

Lời giải

Chọn B

Ta có

Đặt log2 x = t, khi x ∈ (1; 64) thì t ∈ (0; 6)

Khi đó, ta có t2 + t + m ≥ 0 ⇔ m ≥ –t2 –t (*)

Xét hàm số f(t) = –t2 –t với t ∈ (0; 6)

Ta có f’(t) = –2t – 1 < 0, ∀ t ∈ (0; 6)

Ta có bảng biến thiên:

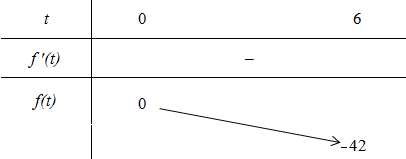
Bất phương trình đã cho đúng với mọi x ∈ (1; 64) khi và chỉ khi bất phương trình (*) đúng với mọi t ∈ (0; 6) ⇔ m ≥ 0.

Bài tập 14. Có bao nhiêu giá trị dương của tham số thực m để bất phương trình có nghiệm duy nhất thuộc [32; +∞)?

A. 2

B. 1

C. 3

D. 0

Lời giải

Chọn D

Điều kiện xác lập

Hàm số xác lập trên [32; +∞)

Đặt t = log2 x. Khi x ≥ 32, ta có miền giá trị của t là [5; +∞).

Bất phương trình có dạng:

Xét hàm số

trên [5; +∞) có nên hàm số nghịch biến trên [5; +∞)

Do

và f (5) = 3 nên ta có một < f(t) ≤ 3

Do với mỗi t có duy nhất một giá trị x nên để bất phương trình đãcho có nghiệm duy nhất thuộc [32; +∞) khi và chỉ bất phương trình

có nghiệm duy nhất trên [5; +∞)

Khi đó:

. Do đó không còn số nguyên dương m thỏa mãn nhu cầu.Bài tập 15. Có bao nhiêu giá trị nguyên dương của tham số m để bất phương trình có nghiệm?

A. 6

B. 4

C. 9

D. 1

Lời giải

Chọn D

Điều kiện: x2 + 3x + m ≥ 0 (*)

Do m nguyên dương nên m = 1 thỏa mãn nhu cầu (*).

Bài tập 16. Tìm toàn bộ những giá trị thực của tham số m để bất phương trình log2 (5x – 1)․log2 (2․5x – 2) ≥ m có nghiệm với mọi x ≥ 1.

A. m ≥ 6

B. m > 6

C. m ≤ 6

D. m < 6

Lời giải

Chọn C

Điều kiện của bất phương trình: x > 0

Ta có log2 (5x – 1)․log2 (2․5x – 2) ≥ m ⇔ log2 (5x – 1)․[1 + log2 (5x – 1)] ≥ m (1)

Đặt t = log2 (5x – 1), với x ≥ 1 ta có t ≥ 2. Khi đó (1) trở thành m ≤ t2 + t (2)

Xét hàm số f(t) = t2 + t trên [2; +∞) ta có f’(t) = 2t + 1 > 0, ∀ t ∈ [2; +∞)

Do đó để bất phương trình đã cho có nghiệm với mọi t ≥ 2 thì

hay m ≤ 6Bài tập 17. Tìm toàn bộ những giá trị thực của tham số m sao cho bất phương trình m․4x + (m – 1)․2x+2 + m – 1 > 0 nghiệm đúng ∀ x ∈ ℝ?

A. m ≤ 3

B. m ≥ 1

C. –1 ≤ m ≤ 4

D. m ≥ 0

Lời giải

Chọn B

Bất phương trình ⇔ m․4x + 4(m – 1)․2x + m – 1 > 0 ⇔ m (4x + 4․2x + 1) > 1 + 4․2x

⇔

Đặt 2x = t (Điều kiện t > 0 ).

Khi đó

Để bất phương trình ban đầu nghiệm đúng ∀ x ∈ ℝ thì bất phương trình

nghiệm đúng ∀ t > 0

Đặt

Hàm số nghịch biến trên (0; +∞). Khi đó

, ∀ t > 0 khi và chỉ khi m ≥ f (0) = 1Bài tập 18. Tìm toàn bộ những giá trị của tham số m bất phương trình 4x–1 – m(2x + 1) > 0 có nghiệm ∀ x ∈ ℝ

A. m ∈ (–∞; 0]

B. m ∈ (0; +∞)

C. m ∈ (0; 1)

D. m ∈ (–∞; 0) ∪ (1; +∞)

Lời giải

Chọn A

Ta có:

Đặt t = 2x, t > 0. Yêu cầu bài toán tương tự với

, ∀ t ∈ (0; +∞)

Đặt

Bảng biến thiên

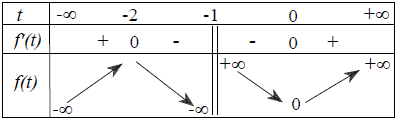
Dựa vào bảng biến thiên có m ≤ 0.

Reply 7 0 Chia sẻ

Share Link Down Cách góp nghiệm bất phương trình miễn phí

Bạn vừa Read Post Với Một số hướng dẫn một cách rõ ràng hơn về Clip Cách góp nghiệm bất phương trình tiên tiến và phát triển nhất và Chia Sẻ Link Cập nhật Cách góp nghiệm bất phương trình Free.

Thảo Luận vướng mắc về Cách góp nghiệm bất phương trình

Nếu sau khi đọc nội dung bài viết Cách góp nghiệm bất phương trình vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha #Cách #góp #nghiệm #bất #phương #trình