Thủ Thuật về Cho tứ giác ABCD biết a 80 độ B 65 độ C 110 độ khi đo góc ngoài tại đỉnh B có số đo là Mới Nhất
You đang tìm kiếm từ khóa Cho tứ giác ABCD biết a 80 độ B 65 độ C 110 độ khi đo góc ngoài tại đỉnh B có số đo là được Cập Nhật vào lúc : 2022-04-20 04:35:12 . Với phương châm chia sẻ Bí quyết về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi Read nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Admin lý giải và hướng dẫn lại nha.Cho hình vẽ dưới đây. Chọn xác lập sai.
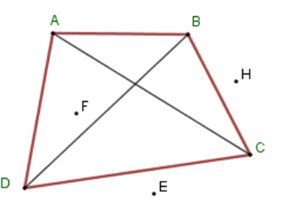
Cho hình vẽ sau. Chọn câu sai.
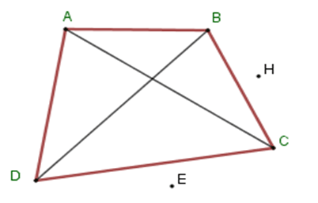
Tứ giác (ABCD) có (widehat C + widehat D = 90^circ .) Chọn câu đúng.
Sách Giải Sách Bài Tập Toán 8 Bài 1: Tứ giác giúp bạn giải những bài tập trong sách bài tập toán, học tốt toán 8 sẽ hỗ trợ bạn rèn luyện kĩ năng suy luận hợp lý và hợp logic, hình thành kĩ năng vận dụng kết thức toán học vào đời sống và vào những môn học khác:
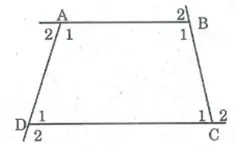
Lời giải:
Ta có: ∠A1 + ∠B1 + ∠C1 + ∠D1 = 360o (tổng những góc của tứ giác)
Tại mỗi đỉnh của tứ giác tổng một góc trong và một góc ngoài bằng 180o nên:
∠A1 + ∠A2 + ∠B1 + (∠B2 + ∠C1 + ∠C2 + ∠D1 + ∠D2 = 180o.4 = 720o
⇒ ∠A2 + (∠B2 +∠C2 + ∠D2 = 720o – (∠A1 +∠B1 +∠C1 + ∠D1 )
= 720o – 360o = 360o
a. Chứng minh rằng BD là đường trung trực của AC.
b. Cho biết B = 100o, D = 70o, tính góc A và góc C.
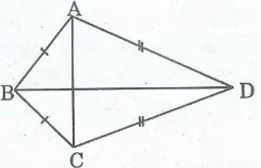
Lời giải:
a. Ta có: BA = BC (gt). Suy ra điểm B thuộc đường trung trực của AC.
Lại có: DA = DC (gt). Suy ra điểm D thuộc đường trung trực của AC.
Vì B và D là 2 điểm phân biệt cùng thuộc đường trung trực của AC nên đường thẳng BD là đường trung trực của AC.
b. Xét ΔBAD và ΔBCD, ta có:
BA = BC (gt)
DA = DC (gt)
BD cạnh chung
Suy ra: ΔBAD = ΔBCD (c.c.c)
⇒ ∠(BAD) = ∠(BCD)
Mặt khác, ta có: ∠(BAD) + ∠(BCD) + ∠(ABC) + ∠(ADC) = 360o
Suy ra: ∠(BAD) + ∠(BCD) = 360o – (∠(ABC) + ∠(ADC) )
2∠(BAD) = 360o – (100o + 70o) = 190o
⇒ ∠(BAD) = 190o : 2 = 95o
⇒ ∠(BCD) = ∠(BAD) = 95o
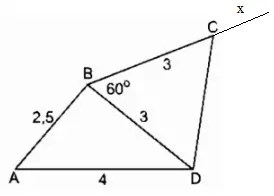
Lời giải:
– Vẽ tam giác ABD
+ Vẽ cạnh AD dài 4cm
+ Tại A vẽ cung tròn tâm A bán kính 2,5cm
+ Tại D vẽ cung tròn tâm D bán kính 3cm
+ Hai cung tròn cắt nhau tại B
⇒ Ta được tam giác ABD
– Vẽ tam giác DBC
+ Dùng thước đo độ vẽ tia Bx sao cho góc DBx = 60o
+ Trên Bx xác lập C sao cho BC = 3cm
⇒ Ta được tam giác BDC
⇒Ta được tứ giác ABCD cần vẽ
Lời giải:
Theo bài ra, ta có:
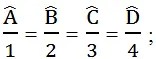∠A+ ∠B+ ∠C+ ∠D= 360o (tổng những góc của tứ giác)
Theo tính chất của dãy tỉ số bằng nhau, ta có:
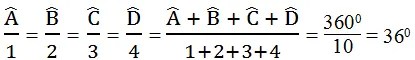
Vậy: ∠A= 1.36o = 36o; ∠B= 2.36o = 72o;
∠C= 3.36o = 108o ; ∠D= 4.36o = 144o.
Lời giải:
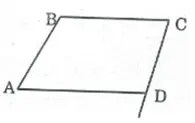
Trong tứ giác ABCD, ta có:
∠A + ∠B + ∠C + ∠D = 360o (tổng những góc của tứ giác)
⇒ ∠D = 360o – (∠A + ∠B + ∠C )
= 360o – (65o + 117o + 71o) = 107o
∠D + ∠D1 = 180o (2 góc kề bù) ⇒ ∠D1 = 180o – ∠D1 = 180o – 107o = 73o
Lời giải:
Giả sử cả bốn góc của tứ giác đều là góc nhọn thì tổng bốn góc của tứ giác nhỏ hơn 360o. Vậy bốn góc của tứ giác không thể đều là góc nhọn. Giả sử cả bốn góc của tứ giác đều la góc tù thì tổng bốn góc của tứ giác to nhiều hơn 360o. Vậy bốn góc của tứ giác không thể đều là góc tù.
Lời giải:
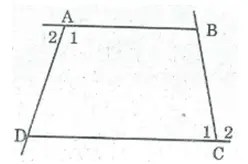
* Gọi ∠A1, ∠C1là góc trong của tứ giác tại đỉnh A và C, ∠A2, ∠C2là góc ngoài tại đỉnh A và C.
Ta có: ∠A1+ ∠A2 = 180o (2 góc kề bù)
⇒ ∠A2= 180o – ∠A1
∠C1+ ∠C2= 180o (2 góc kề bù) ⇒ ∠C2= 180o – ∠C1
Suy ra: ∠A2+ ∠C2= 180o – ∠A1+ 180o – ∠C1= 360o – (∠A1 + ∠C1) (1)
* Trong tứ giác ABCD ta có:
∠A1+ B + ∠C1 + ∠D = 360o (tổng những góc của tứ giác)
⇒ ∠B + ∠D = 360o – ∠A1 + ∠C1 (2)
Từ (1) và (2) suy ra: ∠A2+ ∠C2 = ∠B + ∠D
Lời giải:
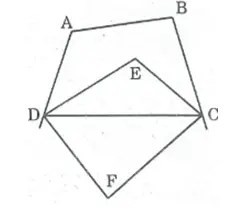
Trong tứ giác ABCD, ta có:
A + B + C + D = 360o
⇒ C + D = 360o – (A + B )
= 360o – (110o + 10o0 ) = 150o
C1 + D1 = (C + D )/2 = 150o/2 = 75o
Trong Δ CED ta có:
(CED) = 180o – (C1 + D1 ) = 180o – 75o = 105o
DE ⊥ DF (t/chất tia phân giác của hai góc kề bù) ⇒ (EDF) = 90o
CE ⊥ CF (t/chất tia phân giác của hai góc kề bù) ⇒ (ECF) = 90o
Trong tứ giác CEDF, ta có: (DEC) + (EDF) + (DFC) + (ECF) = 360o
⇒ (DFC) = 360o – ((DEC) + (EDF) + (ECF) )
(DFC) = 360o – (105o + 90o + 90o) = 750
Lời giải:
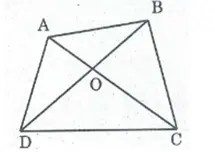
Gọi O là giao điểm của hai tuyến phố chéo AC và BD
* Trong ΔOAB, ta có:
OA + OB > AB (bất đẳng thức tam giác) (1)
* Trong ΔOCD, ta có:
OC + OD > CD (bất đẳng thức tam giác) (2)
Cộng từng vế (1) và (2):
OA + OB + OC + OD > AB + CD
⇒ AC + BD > AB + CD
Lời giải:
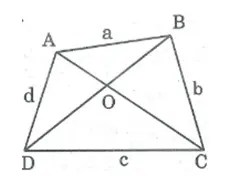
Đặt độ dài a = AB, b = BC, c = CD, d = AD
Gọi O là giao điểm 2 đường chéo AC và BD.
* Trong ΔOAB, ta có:
OA + OB > a (bất đẳng thức tam giác) (1)
* Trong ΔOCD, ta có:
OC + OD > c (bất đẳng thức tam giác) (2)
Từ (1) và (2) suy ra:
OA + OB + OC + OD > a + c hay AC + BD > a + c (*)
* Trong ΔOAD, ta có: OA + OD > d (bất đẳng thức tam giác) (3)
* Trong ΔOBC, ta có: OB + OC > b (bất đẳng thức tam giác) (4)
Từ (3) và (4) suy ra:
OA + OB + OC + OD > b + d hay AC + BD > b + d (**)
Từ (*) và (**) suy ra: 2(AC + BD) > a + b + c + d
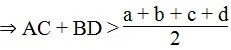
* Trong ΔABC, ta có: AC < AB + BC = a + b (bất đẳng thức tam giác)
* Trong ΔADC, ta có: AC < AD + DC = c + d (bất đẳng thức tam giác)
Suy ra: 2AC < a + b + c + d
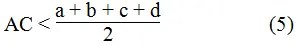
* Trong ΔABD, ta có: BD < AB + AD = a + d (bất đẳng thức tam giác)
* Trong ΔBCD, ta có: BD < BC + CD = b + c (bất đẳng thức tam giác)
Suy ra: 2BD < a + b + c + d
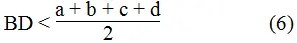
Từ (5) và (6) suy ra: AC + BD < a + b + c + d
A. ∠A = 65o
B. ∠B = 85o
C. ∠C = 100o
D. ∠D = 90o
Lời giải:
Chọn B
Lời giải:
∠A + ∠B = 360o – (60o + 80o) = 220o
∠A – ∠B = 10o
Vậy ∠A = 115o, ∠B = 105o
Lời giải:
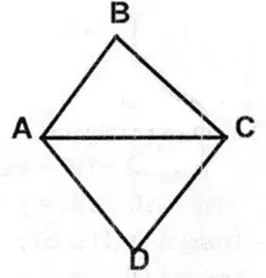
Chu vi ΔABC + chu vi ΔACD – chu vi ABCD = 2AC
⇒ 2AC = 56 + 60 − 66 = 50 (cm)
AC = 25 (cm)
Share Link Down Cho tứ giác ABCD biết a 80 độ B 65 độ C 110 độ khi đo góc ngoài tại đỉnh B có số đo là miễn phí
Bạn vừa đọc tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Video Cho tứ giác ABCD biết a 80 độ B 65 độ C 110 độ khi đo góc ngoài tại đỉnh B có số đo là tiên tiến và phát triển nhất và Chia SẻLink Download Cho tứ giác ABCD biết a 80 độ B 65 độ C 110 độ khi đo góc ngoài tại đỉnh B có số đo là miễn phí.