Kinh Nghiệm về Cho tứ diện đều ABCD có đó dài cạnh bằng a Tính tích vô vị trí hướng của hai vectơ AB và CD Chi Tiết
Bạn đang tìm kiếm từ khóa Cho tứ diện đều ABCD có đó dài cạnh bằng a Tính tích vô vị trí hướng của hai vectơ AB và CD được Update vào lúc : 2022-04-19 00:07:08 . Với phương châm chia sẻ Bí quyết Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Ad lý giải và hướng dẫn lại nha.Trong những mệnh đề sau, mệnh đề nào đúng?
Trong những mệnh đề sau này, mệnh đề nào là đúng?
Mệnh đề nào sau này là đúng?
Cho tứ diện $ABCD$ có trọng tâm $G$. Chọn xác lập đúng?
Cho hình lập phương (ABCD.A'B'C'D'). Chọn xác lập sai?
- lý thuyết
- trắc nghiệm
- hỏi đáp
- bài tập sgk
cho tứ diện đều abcd có cạnh bằng a. tính (overrightarrowAB.overrightarrowBD)
Các vướng mắc tương tự
Mã vướng mắc: 156912
Loại bài: Bài tập
Chủ đề :
Môn học: Toán Học
Câu hỏi này thuộc đề thi trắc nghiệm dưới đây, nhấn vào Bắt đầu thi để làm toàn bài
CÂU HỎI KHÁC
- Cho hình chóp (S.ABC) có (SA) vuông góc (left( ABC right)). Góc giữa (SB) với (left( ABC right)) là góc giữa:
- Cho hình hộp chữ nhật (ABCD.A'B'C'D'). Khi đó, vectơ bằng vectơ (overrightarrowAB) là vectơ nào dưới đây?
- Cho hình chóp (S.ABC) có (ABC)là tam giác vuông tại (B) và (SAbot left( ABC right)). Gọi (AH) là đường cao của tam giác (SAB), thì xác lập nào sau này đúng.
- Cho hình lập phương (ABCD.EFGH) có cạnh bằng (a) . Tính (overrightarrowAB.overrightarrowEG)
- Cho hình chóp (S.ABCD) có đáy (ABCD) là hình thoi tâm (O). Biết (SA=SC,)(SB=SD). Khẳng định nào sau này là sai?
- Cho tam giác ABC vuông cân tại A và BC=a. Trên đường thẳng qua A vuông góc với (left( ABC right)) lấy điểm S sao cho (SA=fracasqrt62). Tính số đo giữa đường thẳng (SA) và (left( ABC right))
- Cho hình chóp đều (S.ABCD) có toàn bộ những cạnh bằng a, điểm M thuộc cạnh SC sao cho (SM=2MC). Mặt phẳng (left( P right)) chứa AM và tuy nhiên tuy nhiên với (BD). Tính diện tích s quy hoạnh thiết diện của hình chóp S.ABCD cắt bởi (left( P right))
- Cho hình lập phương (ABCD.EFGH). Góc giữa cặp vectơ (overrightarrowAB) và (overrightarrowEH) bằng:
- Cho hình chóp (S.ABCD) có đáy (ABCD) là hình chữ nhật, (SAbot left( ABCD right)). Biểu thức nào sau này đúng:
- Cho hình hộp(ABCD.A'B'C'D'). Biểu thức nào sau này đúng:
- Cho hình chóp (S.ABC) có (SB) vuông góc (left( ABC right)). Góc giữa (SC) với (left( ABC right)) là góc giữa:
- Tứ diện đều (ABCD) số đo góc giữa hai véc tơ (overrightarrowAB) và (overrightarrowAD)
- Cho hình lập phương (ABCD.A'B'C'D'). Tính góc giữa hai tuyến phố thẳng AB và A'C'
- Cho hình lập phương (ABCD.A'B'C'D') góc giữa hai tuyến phố thẳng (A'B) và (B'C) là:
- Trong không khí cho đường thẳng D và điểm O. Qua O có mấy mặt phẳng vuông góc với D cho trước?
- Cho hình chóp(S.ABC), gọi (G) là trọng tâm tam giác(ABC). Ta có:
- Cho tứ diện đều (ABCD). Tích vô hướng (overrightarrowAB.overrightarrowCD) bằng:
- Cho hình lập phương (ABCD.A'B'C'D'). Tính góc giữa hai tuyến phố thẳng AB và AD
- Cho hình lăng trụ (ABC.A'B'C'), M là trung điểm của (BB'). Đặt (overrightarrowCA=veca), (overrightarrowCB=vecb), (overrightarrowAA'=vecc). Khẳng định nào sau này đúng?
- Cho hình chóp (S.ABCD) có đáy (ABCD) là hình thoi, (SA) vuông góc với đáy. Biểu thức nào sau này đúng:
- Cho hình chóp (S.ABCD) có toàn bộ những cạnh bên và cạnh đáy đều bằng nhau. Khẳng định nào sau này đúng ?
- Cho hình chóp (S.ABCD) có (SAbot (ABCD)) và đáy là hình vuông vắn. Khẳng định nào sau này đúng?
- Cho hình chóp (S.ABCD) có đáy (ABCD) là hình chữ nhật có (AB=3a,AD=2a), (SA) vuông góc với mặt phẳng (left( ABCD right)), (SA=a). Gọi (varphi ) là góc giữa đường thẳng (SC) và mp (left( ABCD right)). Khi đó (tan varphi ) bằng bao nhiêu?
- Cho hình lập phương (ABCD.EFGH). Hãy xác lập góc giữa cặp vectơ (overrightarrowAB) và(overrightarrowEG)
- Cho hình chóp (S.ABC) có đáy (ABC) là tam giác vuông tại B, cạnh bên (textSA) vuông góc với đáy. Khẳng định nào sau này đúng?
Với Cách tính tích vô vị trí hướng của hai vectơ hay, rõ ràng Toán lớp 11 gồm khá đầy đủ phương pháp giải, ví dụ minh họa và bài tập trắc nghiệm có lời giải rõ ràng sẽ hỗ trợ học viên ôn tập, biết phương pháp làm dạng bài tập tính tích vô vị trí hướng của hai vectơ từ đó đạt điểm trên cao trong bài thi môn Toán lớp 11.

Trong không khí, cho hai vectơ u→ và v→ đều khác 0→ . Tích vô vị trí hướng của hai vectơ u→ và v→ là một số trong những, kí hiệu là u→. v→, được xác lập bởi công thức:

Trong trường hợp u→ = 0→ hoặc v→ = 0→, ta quy ước u→. v→ = 0→
Ví dụ 1: Cho tứ diện đều ABCD, M là trung điểm của cạnh BC. Khi đó cos(AB; DM) bằng :

Hướng dẫn giải
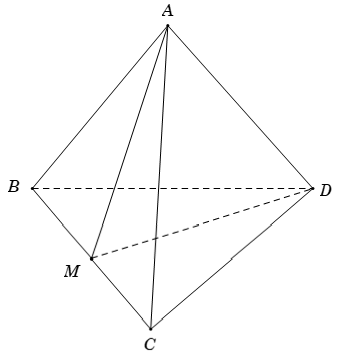
Giả sử cạnh của tứ diện là a.
Tam giác BCD đều ⇒ DM = (a√3)/2.
Tam giác ABC đều ⇒ AM = (a√3)/2.
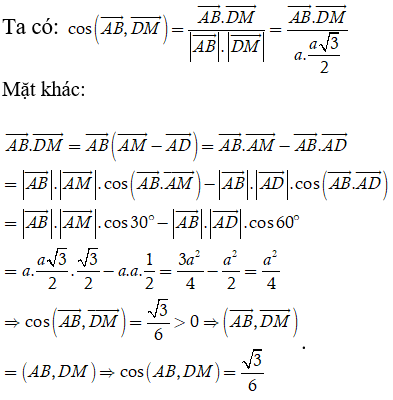
Chọn B.
Ví dụ 2: Cho tứ diện ABCD có AB = AC = AD và ∠BAC = ∠BAD = 60° . Hãy xác lập góc giữa cặp vectơ AB→ và CD→ ?
A. 60° B. 45° C . 120° D. 90°
Hướng dẫn giải
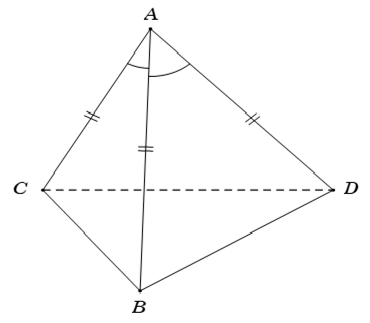

Chọn D
Ví dụ 3: Cho hình chóp S.ABC có SA = SB = SC và  . Hãy xác lập góc giữa cặp vectơ SC→ và AB→ ?
. Hãy xác lập góc giữa cặp vectơ SC→ và AB→ ?
A. 120° B. 45° C. 60° D. 90°
Hướng dẫn giải
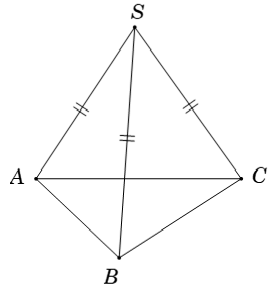

Chọn D
Ví dụ 4: Cho hình chóp S.ABC có SA = SB và CA = CB. Tính số đo của góc giữa hai tuyến phố thẳng chéo nhau SC và AB
A. 30° B. 45° C. 60° D. 90°
Hướng dẫn giải
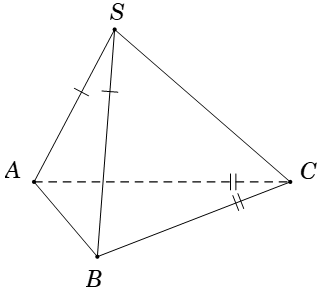
Xét:

Vậy SC và AB vuông góc với nhau
Chọn D
Ví dụ 5: Cho hình chóp S.ABC có AB = AC và ∠SAC = ∠SAB . Tính số đo của góc giữa hai tuyến phố thẳng chéo nhau SA và BC
A. 30° B. 45° C. 60° D. 90°
Hướng dẫn giải

Vậy SA ⊥ BC
Chọn D
Ví dụ 6: Cho tứ diện ABCD. Chứng minh rằng nếu
 thì AB ⊥ CD , AC ⊥ BD, AD ⊥ BC. Điều ngược lại đúng không ạ?
thì AB ⊥ CD , AC ⊥ BD, AD ⊥ BC. Điều ngược lại đúng không ạ?
Sau đấy là lời giải:
Bước 1:
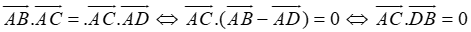
⇔ AC ⊥ BD
Bước 2: Chứng minh tương tự, từ AC→.AD→ = AD→.AB→ ta được AD→ ⊥ BC→ và AB→.AC→ = AD→.AB→ ta được AB→ ⊥ CD→
Bước 3: trái lại đúng, vì quy trình chứng tỏ ở bước 1 và 2 là quy trình biến hóa tương tự
Bài giải trên đúng hay sai? Nếu sai thì sai ở đâu?
A. Sai ở bước 3
B. Đúng
C. Sai ở bước 2
D. Sai ở bước 1
Hướng dẫn giải
Chọn B
Bài giải đúng

Câu 1: Cho tứ diện ABCD có AC = (3/2)AD, ∠CAB = ∠DAB = 60°, CD = AD. Gọi α là góc giữa AB và CD. Chọn xác lập đúng?
A. cosα = (3/4) B. α = 60° C. α = 30° D. cosα = 1/4
Lời giải:


Chọn D
Câu 2: Cho tứ diện ABCD có AB = AC = AD và ∠BAC = ∠BAD = 60°, ∠CAD = 90°. Gọi I và J lần lượt là trung điểm của AB và CD . Hãy xác lập góc giữa cặp vectơ AB→ và IJ→ ?
A. 120° B. 90° C. 60° D. 45°
Lời giải:
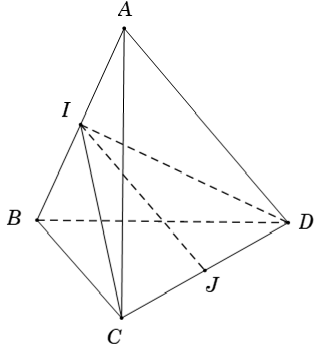
Xét tam giác ICD có J là trung điểm đoạn CD ⇒ IJ→ = (1/2)(IC→ + ID→)
Tam giác ABC có AB = AC và ∠BAC = 60° nên tam giác ABC đều ⇒ CI ⊥ AB (1)
Tương tự, ta có tam giác ABD đều nên DI ⊥ AB (2)
Từ ( 1) và (2) ta có
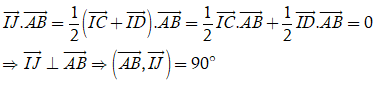
Chọn B
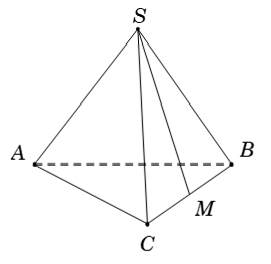
Câu 3: Cho hình chóp S. ABCD có đáy là hình vuông vắn ABCD cạnh bằng a và những cạnh bên đều bằng a. Gọi M và N lần lượt là trung điểm của AD và SD. Số đo của góc (MN ; SC) bằng
A. 45° B. 30° C. 90° D.60°
Lời giải:
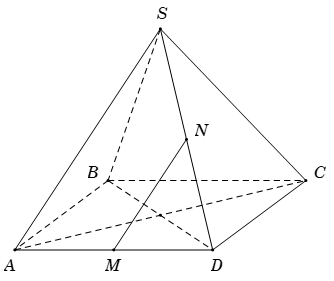
Do ABCD là hình vuông vắn cạnh a ⇒ AC = a√2
Ta có : AC2 = 2a2= SA2 + SC2
⇒ tam giác SAC vuông taị S.
Từ giả thiết ta có MN là đường trung bình của tam giác DSA ⇒ MN→ = (1/2).SA→
Khi đó
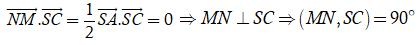
Chọn C
Câu 4: Cho hình lập phương ABCD.EFGH có cạnh bằng a. Tính AB→.EG→

Lời giải:
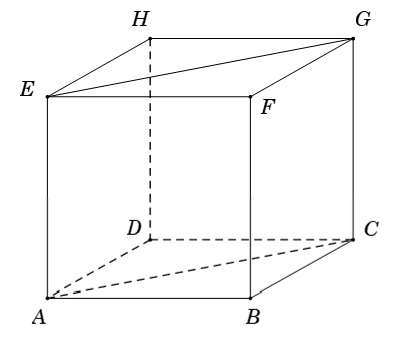
Ta có: EGCA là hình bình hành nên EG→ = AC→ ⇒ AB→.EG→ = AB→.AC→
Mặt khác AC→ = AB→ + AD→ ( quy tắc hình hộp) .
Suy ra
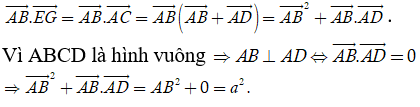
Chọn B

Câu 5: Cho hình lập phương ABCD.A1B1C1D1 có cạnh a. Gọi M là trung điểm AD. Giá trị B1M→.BD1→ là:
Lời giải:

Chọn A
Câu 6: Cho tứ diện đều ABCD. Số đo góc giữa hai tuyến phố thẳng AB và CD bằng:
A. 60° B. 30° C. 90° D. 45°
Lời giải:
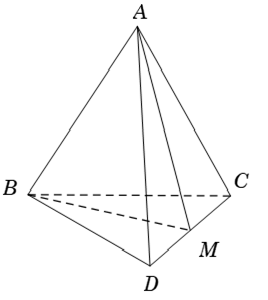
+ Gọi M là trung điểm của CD
+ Tam giác ACD và tam giác BCD là tam giác đều ( vì ABCD là tứ diện đều) có AM ; BM là hai tuyến phố trung tuyến ứng với cạnh CD nên đồng thời là đường cao.
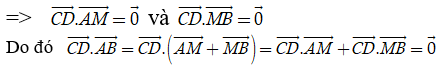
Suy ra AB→ ⊥ CD→ nên số đo góc giữa hai tuyến phố thẳng AB và CD bằng 90°.
Chọn C
Câu 7: Cho tứ diện ABCD đều cạnh bằng a. Gọi O là tâm đường tròn ngoại tiếp tam giác BCD. Góc giữa AO và CD bằng bao nhiêu ?
A. 0° B. 30° C. 90° D. 60°
Lời giải:
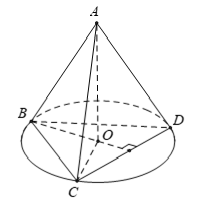

Câu 8: Cho hai vectơ a→ và b→ thỏa mãn nhu cầu:  . Gọi α là góc giữa hai vectơ a→ và b→. Chọn xác lập đúng?
. Gọi α là góc giữa hai vectơ a→ và b→. Chọn xác lập đúng?

Lời giải:
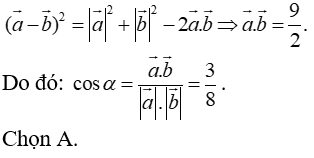
Câu 9: Cho tứ diện ABCD. Tìm giá trị của k thích hợp thỏa mãn nhu cầu:

A. k = 1 B. k = 2 C. k = 0 D. k = 4
Lời giải:
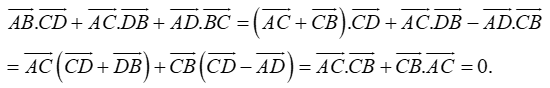
Chọn đáp án C
Câu 10: Trong không khí cho tam giác ABC có trọng tâm G. Chọn hệ thức đúng?
A. AB2 + AC2 + BC2 = 2.(GA2 + GB2 + GC2)
B. AB2 + AC2 + BC2 = GA2 + GB2 + GC2
C. AB2 + AC2 + BC2 = 4.(GA2 + GB2 + GC2)
D. AB2 + AC2 + BC2 = 3.(GA2 + GB2 + GC2)
Lời giải:
Cách 1
Ta có
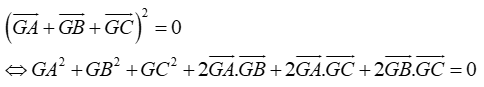


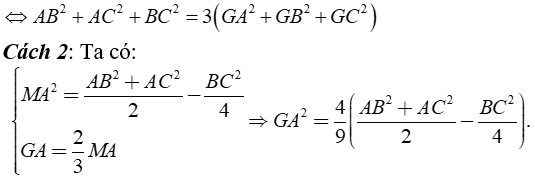
Tương tự ta suy ra được GA2 + GB2 + GC2
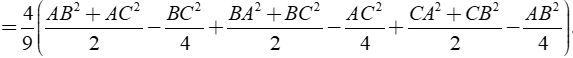

Chọn đáp án D.
Share Link Download Cho tứ diện đều ABCD có đó dài cạnh bằng a Tính tích vô vị trí hướng của hai vectơ AB và CD miễn phí
Bạn vừa tìm hiểu thêm tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Video Cho tứ diện đều ABCD có đó dài cạnh bằng a Tính tích vô vị trí hướng của hai vectơ AB và CD tiên tiến và phát triển nhất và Chia SẻLink Tải Cho tứ diện đều ABCD có đó dài cạnh bằng a Tính tích vô vị trí hướng của hai vectơ AB và CD Free.