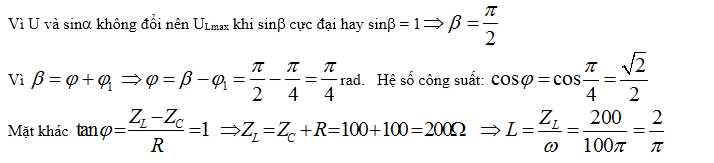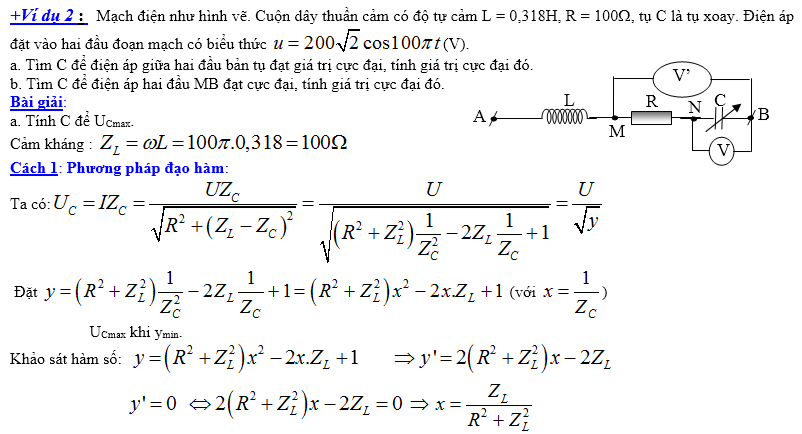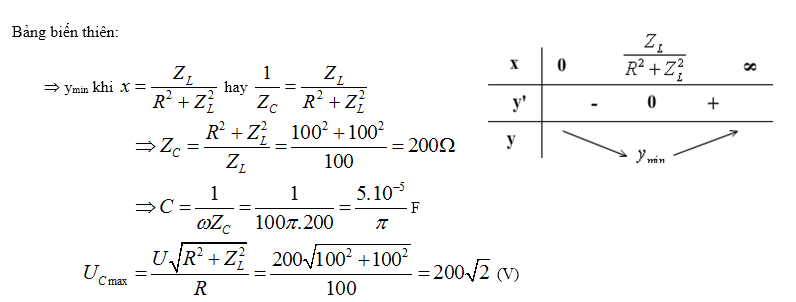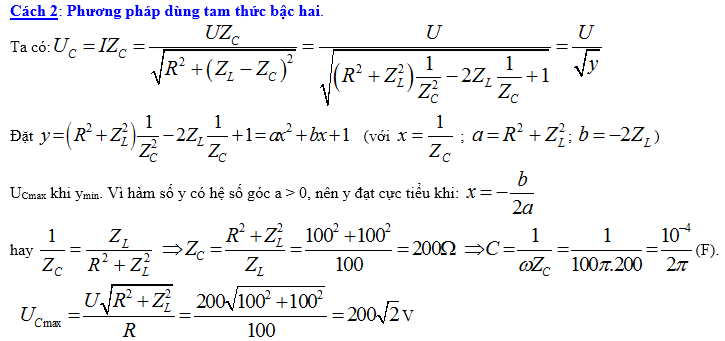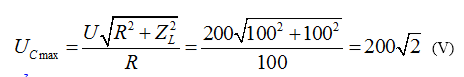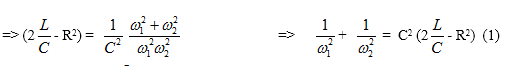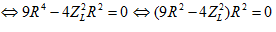Thủ Thuật Hướng dẫn Đặt một điện áp xoay chiều có tần số f thay đổi và giá trị hiệu dụng 30V Chi Tiết
You đang tìm kiếm từ khóa Đặt một điện áp xoay chiều có tần số f thay đổi và giá trị hiệu dụng 30V được Cập Nhật vào lúc : 2022-04-06 03:05:11 . Với phương châm chia sẻ Mẹo về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm tài liệu vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Mình lý giải và hướng dẫn lại nha.
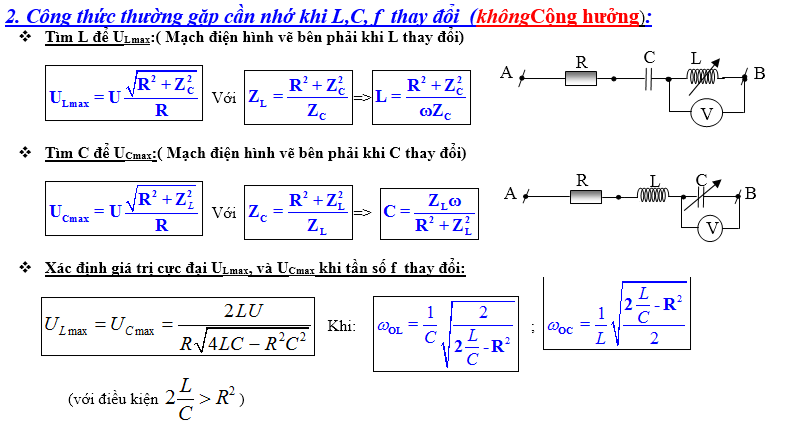
1.Các công thức của những điện áp hiệu dụng cực lớn khi thông số của mạch thay đổi:
a. Điện áp hiệu dụng UR:
+ R thay đổi : UR(max) = U Khi R [to infty ]
+ L,hay C, hay [omega ] thay đổi : UR(max) = U Khi [omega =frac1sqrtLC] ( Cộng hưởng )
b. Điện áp hiệu dụng : UL
+ R thay đổi : UL(max) = [fracU Z_L-Z_C rightZ_L] khi R = 0
+ L thay đổi : UL(max) = IZL = [fracUsqrtR^2+Z_C^2R] khi ZL = [fracR^2+Z_C^2Z_C]
+ C thay đổi : UL(max) = IZL = [fracURZ_L] khi C = [frac1Lomega ^2] ( Cộng hưởng )
+ [omega ] thay đổi : UL(max) = IZL khi [omega ] = [sqrtfrac22LC-R^2C^2]
c. Điện áp hiệu dụng : UC
+ R thay đổi : UC(max) = [fracUZ_C] khi R = 0
+ C thay đổi : UC(max) = IZC = [fracUsqrtR^2+Z_L^2R] khi ZC = [fracR^2+Z_L^2Z_L]
+ L thay đổi : UC(max) = IZC = [fracURZ_C] khi L = [frac1Comega ^2] ( Cộng hưởng )
+ [omega ] thay đổi : UC(max) = IZC khi [omega ] = [sqrtfrac1LC-fracR^22L^2]
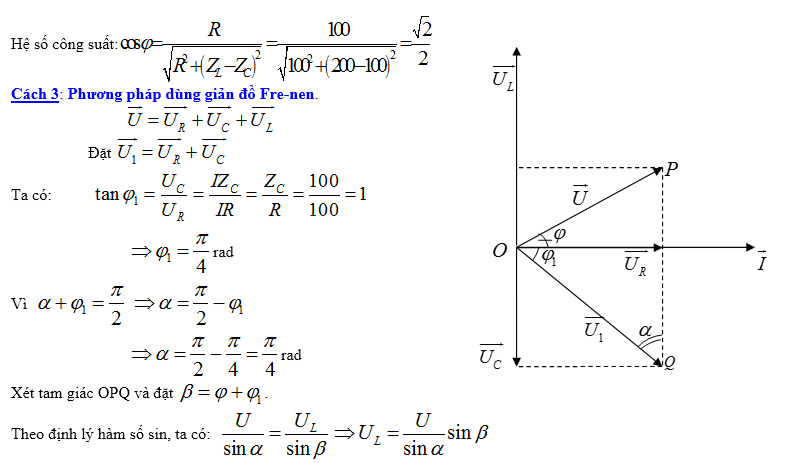
+Ví dụ 3 : Đặt điện áp xoay chiều u=U0coswt (U0 không đổi và w thay đổi được) vào hai đầu đoạn mạch gồm điện trở thuần R,cuộn cảm thuần có độ tự cảm L và tụ điện có điện dung C mắc tiếp nối đuôi nhau,với CR2< 2L. Khi w = w1 hoặc w = w2 thì điện áp hiệu dụng giữa hai đầu cuộn cảm có cùng một giá trị.Khi w = w0 thì điện áp hiệu dụng giữa hai đầu cuộn cảm có mức giá trị cực lớn.Hệ thức liên hệ giữa w1,w2 và w0 là :
A.$omega _0^2=frac12(omega _1^2+omega _2^2)$ B.$omega _0^=frac12(omega _1^+omega _2^)$ C.$frac1omega _0^2$ =$frac12$ ($frac1omega _1^2$+$frac1omega _2^2$) D. w0 = $sqrtomega _1omega _2$
Giải:
Giải: UL = $fracUZ_LsqrtR^2+(Z_L-Z_C)^2$. Do UL1 = UL2 => $fracomega _1^2R^2+(omega _1^L-frac1omega _1^C)^2$ = $fracomega _2^2R^2+(omega _2L-frac1omega _2C)^2$
=> $fracR^2-2fracLComega _1^2$ + $frac1omega _1^4C^2$= $fracR^2-2fracLComega _2^2$ + $frac1omega _2^4C^2$=> (2$fracLC$- R2)($frac1omega _2^2$-$frac1omega _1^2$) = $frac1omega _2^4C^2$-$frac1omega _1^4C^2$
UL = ULmax khi $fracR^2-2fracLComega ^2$ + $frac1omega ^4C^2$ + L2 có mức giá trị cực tiểu. => $frac1omega _0^2$= $fracC^22$(2$fracLC$- R2) (2)
Từ(1) và (2) suy ra:$frac1omega _0^2$ =$frac12$ ($frac1omega _1^2$+$frac1omega _2^2$) . Chọn đáp án C. Với Đk CR2< 2L
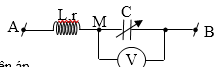
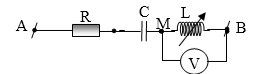
Ví dụ 5: Cho mạch điện như hình vẽ. Cuộn dây có độ tự cảm
[L=fracsqrt3pi ]H, điện trở thuần r = 100W. Đặt vào hai đầu đoạn mạch một điện áp
[u_AB=100sqrt2cos 100pi t](V). Tính giá trị của C để vôn kế có mức giá trị lớn số 1 và tìm giá trị lớn số 1 đó của vôn kế.
A. [C=frac4sqrt3pi .10^-4]F và [U_Cmax =120]V. B. [C=fracsqrt34pi .10^-4]F và [U_Cmax =180]V.
C. [C=fracsqrt34pi .10^-4]F và [U_Cmax =200]V. D. [C=fracsqrt3pi .10^-4]F và [U_Cmax =220]V.
Giải. Ta có: [Z_L=omega L=100pi .fracsqrt3pi =100sqrt3Omega ].
[U_Cmax Leftrightarrow Z_C=fracr^2+Z_L^2Z_L=frac100^2+left( 100sqrt3 right)^2100sqrt3=frac400sqrt3Omega ].[Rightarrow C=frac1omega Z_C=frac1100pi .frac400sqrt3=fracsqrt34pi .10^-4]F.;
[U_Cmax =fracUsqrtr^2+Z_L^2R=frac100sqrt100^2+left( 100sqrt3 right)^2100=200]V. Chọn C.
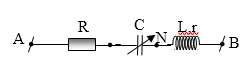
+Ví dụ 6: Cho đoạn mạch điện xoay chiều ANB , tần số dòng điện 50Hz, đoạn AN chứa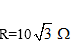 
và C thay đổi ,đoạn NB Chứa L=$frac0.2pi $ H .Tìm C để $U_AN$ cực lớn :
: A.C=106$mu F$ B.200$mu F$
C.300$mu F$ D.250$mu F$
Giải: Dùng công thức: Khi $Z_C=fracZ_L+sqrt4R^2+Z_L^22$ thì $U_RCMtextax=frac2UtextRsqrt4R^2+Z_L^2-Z_L$ = UAN
Lưu ý: R và C mắc liên tục nhau; Z L= w.L = 100p.0,2/p. =20W
Tính : $Z_C=fracZ_L+sqrt4R^2+Z_L^22$=$=frac20+sqrt4(10sqrt3)^2+20_^22=frac20+sqrt1200+4002=30Omega $
Mà $Z_C=frac1omega C=>C=frac1omega .Z_C=frac1100pi .30=frac10^-33pi (F)$ = 106$mu F$ Đáp án A
+Ví dụ 7: Cho đoạn mạch điện xoay chiều ANB ,đoạn AN chứa R và C thay đổi ,đoạn NB Chứa L=$frac1.5pi $ H . Biết f=50Hz ,người ta thay đổi C sao cho$U_AN$ cực lớn bằng 2$U_AB$ .Tìm R và C:
A. $Z_C$=200 $Omega $; R=100$Omega $ B. $Z_C$=100 $Omega $; R=100$Omega $
C. $Z_C$=200 $Omega $; R=200$Omega $ D. $Z_C$=100 $Omega $; R=200$Omega $
Giải: Khi $Z_C=fracZ_L+sqrt4R^2+Z_L^22$ thì $U_RCMtextax=frac2UtextRsqrt4R^2+Z_L^2-Z_L$ Lưu ý: R và C mắc liên tục nhau
Đề cho $U_AN$ cực lớn bằng 2$U_AB$ suy ra: $1=fractextRsqrt4R^2+Z_L^2-Z_L$ => $4R^2+Z_L^2-2Z_Lsqrt4R^2+Z_L^2.+Z_L^2=R^2$
$Leftrightarrow 3R^2+2Z_L^2=2Z_Lsqrt4R^2+Z_L^2=>9R^4+12(R^2Z_L^2)+4Z_L^4=4Z_L^2(4R^2+Z_L^2)_$
$Leftrightarrow 9R^4+(12Z_L^2-16Z_L^2)R^2=0$
Do R khác 0 nên $Leftrightarrow (9R^2-4Z_L^2)=0$ => $Leftrightarrow (9R^2-4Z_L^2)=0=>R=frac23Z_L^=frac23150=100Omega $
$Z_C=fracZ_L+sqrt4R^2+Z_L^22$ =$=frac150+sqrt4100^2+150_^22=200Omega $ Đáp án A
+Ví dụ 8: Đặt một điện áp xoay chiều u = U0coswt (V) vào hai đầu một đoạn mạch AB gồm điện trở R, cuộn dây cảm thuần L và tụ điện có điện dung C mắc tiếp nối đuôi nhau. Tụ C có điện dung thay đổi được.Thay đổi C, khi ZC = ZC1 thì cường độ dòng điện trễ pha $fracpi 4$ so với điện áp hai đầu đoạn mạch, khi ZC = ZC2 = 6,25ZC1 thì điện áp hiệu
dụng giữa hai tụ đạt giá trị cực lớn. Tính thông số hiệu suất của mạch.
A. 0,6 B. 0,8 C. 0,7 D. 0,9
Giải: tanj1 = $fracZ_L-Z_C1R$= tan($fracpi 4$) = 1=> R = ZL – ZC1 => ZC1 = ZL - R
Ta có: UC2 = Ucmax => ZC2 = $fracR^2+Z_L^2Z_L$=> 6,25ZC1ZL = R2 +ZL2
=> 6,25( ZL- R) ZL = R2 +ZL2 => 5,25ZL2 - 6,25RZL – R2 = 0 => 21ZL2 - 25RZL – 4R2 = 0 => ZL = $frac4R3$
Ta có: ZC2 = $fracR^2+Z_L^2Z_L$= $fracR^2+frac16R^29frac4R3$ = $frac25R12$=> cosj2 = $fracRZ_2$ = $fracRsqrtR^2+(frac4R3-frac25R12)^2$= 0,8. Chọn đáp án B
+Ví dụ 9: Cho mạch điện RLC, Với C thay đổi được. Điện áp đặt vào hai đầu đoạn mạch có dạng $u=Usqrt2cos omega t(V).$ Khi $C=C_1=frac10^-4pi (F)text $ thì cường độ dòng điện i trễ pha $fracpi 4$ so với u. Khi $C=C_2=frac10^-42,5pi (F)text $thì điện áp hai đầu tụ điện đạt giá trị cực lớn. Tính tần số góc $omega $. Biết $L=frac2pi (H)$
A. $200pi (rad/s)$ B. $50pi (rad/s)$ C. $10pi (rad/s)$ D. $100pi (rad/s)$
Giải: Khi $C=C_1=frac10^-4pi (F)text $ thì dòng điện i trễ pha $fracpi 4$ so u nên: $Z_L-Z_C1=R$ (1)
Khi $C=C_2=frac10^-42,5pi (F)text $thì điện áp hai đầu tụ điện đạt giá trị cực lớn nên :$Z_C2=fracR^2+Z_L^2Z_L$ (2)
thay (1) vào (2) ta có pt:$frac8pi ^2omega ^4-9.10^4omega ^2+10^8pi ^2=0$ (3)
-giải ta đươc: $omega =100pi $rad/s và $omega =frac50pi sqrt2$ Rad/s (loại) vì thay nghiệm này vào (1) thì không thỏa mãn nhu cầu
+Ví dụ 10: Cho mạch điện xoay chiều RLC mắc tiếp nối đuôi nhau. Điện áp xoay chiều đặt vào hai đầu đoạn mạch có biểu thức [u=Usqrt2ctextosomega t,] tần số góc $omega $ biến hóa. Khi [omega =omega _1=40pi (rad/s)] và khi [omega =omega _2=360pi (rad/s)] thì cường độ dòng điện hiệu dụng qua mạch điện có mức giá trị bằng nhau. Để cường độ dòng điện trong mạch đạt giá trị lớn số 1 thì tần số góc $omega $ bằng
A 100$pi $(rad/s). B 110$pi $(rad/s).
C 200$pi $(rad/s). D 120$pi $(rad/s).
Giải 1: Nhớ công thức:Với w = w1 hoặc w = w2 thì I hoặc P hoặc UR có cùng một giá trị thì IMax hoặc PMax hoặc URMax
khi đó ta có: $omega =sqrtomega _1omega _2$=120$pi $(rad/s). Chọn D
Giải 2: I1 = I1 => Z1 = Z1 => (ZL1 – ZC1)2 = (ZL2 – ZC2)2
Do w1 ¹ w2 nên (ZL1 – ZC1) = - (ZL2 – ZC2) => ZL1 + ZL2 = ZC1 + ZC2
(w1 + w2)L = $frac1C$ ($frac1omega _1$+$frac1omega _2$) => LC = $frac1omega _1omega _2$ (1)
Khi I = Imax; trong mạch có cộng hưởng LC = $frac1omega ^2$ (2). Từ (1) và (2) ta có w =$sqrtomega _1omega _2$ = 120p.(rad/s). Chọn D
+Ví dụ 11: Đặt một điện áp u = U0 cos[omega t]( U0 không đổi, [omega ] thay đổi được) vào 2 đầu đoạn mạch gồm R, L, C mắc tiếp nối đuôi nhau thỏa mãn nhu cầu Đk: CR2 < 2L. Gọi V1,V2, V3 lần lượt là những vôn kế mắc vào 2 đầu R, L, C. Khi tăng dần tần số thì thấy trên mỗi vôn kế đều phải có một giá trị cực lớn, thứ tự lần lượt những vôn kế chỉ giá trị cực lớn khi tăng dần tần số là
A. V1, V2, V3. B. V3, V2, V1. C. V3, V1, V2. D. V1, V3,V2.
Giải: Ta gọi số chỉ của những vôn kế là U: U1=IR =$fracURsqrtR^2+(omega L-frac1omega C)^2$
U1 = U1max khi trong mạch có sự cộng hưởng điện: => w2 = $frac1LC$ (1)
U2 = IZL =$fracUomega LsqrtR^2+(omega L-frac1omega C)^2=fracULsqrtfracR^2+omega ^2L^2+frac1omega ^2C^2-2fracLComega ^2=fracUy_2^2$
U2 = U2max khi y2 = $frac1C^2frac1omega ^4+fracR^2-2fracLComega ^2+L^2$có mức giá trị cực tiểu y2min
Đặt x = $frac1omega ^2$, Lấy đạo hàm y2 theo x, cho y2’ = 0 => x = $frac1omega ^2$=$fracC2(2fracLC-CR^2)$
$omega _2^2=frac2C^2(2fracLC-R^2)$=$frac2C(2L-CR^2)$ (2)
U3 = IZC =$fracUomega CsqrtR^2+(omega L-frac1omega C)^2=fracUCsqrtomega ^2(R^2+omega ^2L^2+frac1omega ^2C^2-2fracLC)=fracUy_3^2$
U3 = U3max khi y3 = L2w4 +(R2 -2$fracLC$ )w2 + $frac1C^2$ có mức giá trị cực tiểu y3min
Đặt y = w2 , Lấy đạo hàm của y3 theo y, cho y’3 = 0
y = w2 = $frac2fracLC-R^22L^2=frac1LC-fracR^22L^2$ => w32 =$frac1LC-fracR^22L^2$ (3)
So sánh (1); (2), (3): Do CR2 < 2L nên : 2L – CR2 > 0
Từ (1) và (3) w32 =$frac1LC-fracR^22L^2$ < >w12 = $frac1LC$
Xét hiệu w22 - w12 = $frac2C(2L-CR^2)$-$frac1LC$=$frac2L-(2L-CR^2)LC(2L-R^2)=fracCR^2LC(2L-R^2)$> 0
Do đó w22 = $frac2C(2L-CR^2)$ > w12 = $frac1LC$
Vậy ta có w32 =$frac1LC-fracR^22L^2$ < >w12 = $frac1LC$ < >w22 = $frac2C(2L-CR^2)$
Khi tăng dần tần số thì những vôn kế chỉ số cực lớn lần lượt là V3, V1 và V2. Chọn đáp án C
+Ví dụ 12: Đặt điện áp xoay chiều có f thay đổi vào hai đầu đoạn mạch điện xoay chiều RLC mắc theo thứ tự đó có R=50W,$L=frac16pi H;C=frac10^-224pi F$ . Để điện áp hiệu dụng 2 đầu LC (ULC) đạt giá trị cực tiểu thì tần số dòng điện phải bằng
A. 60 Hz B. 50 H C. 55 Hz D. 40 Hz
Giải: Ta có $U_LC=Ileft| Z_L-Z_C right|=fracUsqrtR^2+(Z_L-Z_C)^2left| Z_L-Z_C right|=fracUfracsqrtR^2+(Z_L-Z_C)^2=fracUsqrtfracR^2(Z_L-Z_C)^2+1$
Muốn ULC cực tiểu thì $fracR^2(Z_L-Z_C)^2+1$ cực lớn khi $Z_L=Z_Cleftrightarrow LComega ^2=1$
$leftrightarrow frac16pi frac10^-224pi 4pi ^2f^2=1leftrightarrow f=sqrtfrac6.244.10^-2=60Hz$
4. Bài tập trắc nghiệm:
Câu 1:Một đoạn mạch RLC không phân nhánh gồm điện trở thuần 100$Omega $, cuộn dây cảm thuần có độ tự cảm $frac1pi H$ và tụ điện có điện dung C thay đổi được. Đặt vào hai đầu đoạn mạch một điện áp [u=200sqrt2cos 100pi t(V)]. Thay đổi điện dung C của tụ điện cho tới lúc điện áp hiệu dụng giữa hai đầu tụ điện đạt giá trị cực lớn. Giá trị cực lớn đó bằng:
A. $100sqrt2V$ B. 200[sqrt2]V C. $50sqrt2V$ D. 100V
Câu 2: Cho đoạn mạch điện không phân nhánh RLC. Điện áp giữa hai đầu đoạn mạch có biểu thức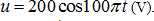 
Điện trở R = 100W, Cuộn dây thuần cảm có L thay đổi được, tụ điện có điện dung 
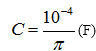. Xác định L sao cho điện áp hiệu dụng giữa hai đầu cuộn dây đạt giá trị cực lớn.
A. L= [frac1pi ]H B. L= [frac2pi ]H C. L= [frac0,5pi ]H D. L= [frac0,1pi ]H
Câu 3:Mạch điện xoay chiều tiếp nối đuôi nhau gồm cuộn dây có độ tự cảm L, điện trở r và tụ điện C. Đặt vào hai đầu đoạn mạch một hiệu điện thế xoay chiều có mức giá trị hiệu dụng 30V.Điều chỉnh C để điện áp trên hai bản tụ đạt giá trị cực lớn và bằng số 50V. Điện áp hiệu dụng giữa hai đầu cuộn dây khi đó là bao nhiêu?
A. 30V B. 20V C. 40V D. 50V
Câu 4: Đặt điện áp xoay chiều có f thay đổi vào hai đầu đoạn mạch điện xoay chiều RLC mắc theo thứ tự đó có R=50W,$L=frac16pi H;C=frac10^-224pi F$ . Để điện áp hiệu dụng 2 đầu LC (ULC) đạt giá trị cực tiểu thì tần số dòng điện phải bằng:
A. 60 Hz B. 50 Hz C. 55 Hz D. 40 Hz
Câu 5: Một mạch điện xoay chiều mắc tiếp nối đuôi nhau gồm một điện trở, một tụ điện và một cuộn dây thuần cảm có thông số tự cảm L hoàn toàn có thể thay đổi, với u là điện áp hai đầu đoạn mạch và uRC là điện áp hai đầu đoạn mạch chứa RC, thay đổi L để điện áp hiệu dụng hai đầu cuộn dây đạt giá trị cực lớn khi đó kết luận nào sau này là sai?
A. u và uRC vuông pha. B. u và uRC cùng pha. C. $Z_L=fracZ_C^2+R^2Z_C$ D. $(U_L)_Max=fracUsqrtR^2+Z_C^2Z_C$
.Câu 6: Cho mạch điện gồm R, L, C mắc tiếp nối đuôi nhau. Biết R = 30Ω, ZL = 40Ω, còn C thay đổi được. Đặt vào hai đầu mạch điện một điện áp u = 120cos(100t - π/4)V. Khi C = Co thì điện áp hiệu dụng giữa hai bản tụ đạt giá trị cực lớn UCmax bằng
A. UCmax = 100$sqrt2$V B. UCmax = 36$sqrt2$V C. UCmax = 120V D. UCmax = 200 V
Câu 7: (ĐH-2011) Đặt điện áp xoay chiều $u=Usqrt2cos 100pi t$ (U không đổi, t tính bằng s) vào hai đầu đoạn mạch mắc tiếp nối đuôi nhau gồm điện trở thuần R, cuộn cảm thuần có độ tự cảm $frac15pi $ H và tụ điện có điện dung C thay đổi được. Điều chỉnh điện dung của tụ điện để điện áp hiệu dụng giữa hai bản tụ điện đạt giá trị cực lớn. Giá trị cực lớn đó bằng $Usqrt3$. Điện trở R bằng
A. $20sqrt2$ $Omega $. B. $10sqrt2$ $Omega $. C. 10 $Omega $. D. 20 $Omega $.
Giải:Ta có:ZL = ω.L= 20Ω; Ucmax = $fracUsqrtR^2+Z_L^2R=Usqrt3to sqrtR^2+Z_L^2=Rsqrt3to R=fracZ_Lsqrt2=10sqrt2Omega $ Þ Đáp án B.
Câu 8: Cho mạch điện xoay chiều không phân nhánh RLC có tần số thay đổi được.Gọi f0 ;f1 ;f2 lần lượt những giá trị tần số làm cho hiệu điện thế hiệu dung hai đầu điện trở cực lớn, hiệu điện thế hiệu dung hai đầu cuộn cảm cực lớn, hiệu điện thế hiệu dung hai đầu tụ điện cực lớn.Ta có :
A.f0=$fracf_1f_2$ B.f0=$fracf_2f_1$ C.f1.f2=f02 D. f0 =f1 + f2
Câu 9: Một mạch điện xoay chiều gồm một tụ điện C tiếp nối đuôi nhau với một cuộn dây. Đặt vào hai đầu đoạn mạch một hiệu điện thế u = 100$sqrt2$coswt(V) thì hiệu điện thế hiệu dụng hai đầu tụ điện C và hai đầu cuộn dây lần lượt là 100$sqrt2$(V) và 100 V. Cường độ hiệu dụng trong mạch I =$sqrt2$(A). Tính tần số góc w, biết rằng tần số xấp xỉ riêng của mạch w0 =100$sqrt2$π ( rad/s).
A. 100π ( rad/s). B.50π ( rad/s). C. 60π ( rad/s). D. 50$sqrt2$π ( rad/s).
Câu 10: Cho đoạn mạch điện AB gồm mạch AM mắc tiếp nối đuôi nhau với mạch MB. Mạch AM chỉ chứa cuộn cảm thuần có độ tự cảm L = $fractext1text2 !!pi!!text $H; mạch MB gồm điện trở hoạt động và sinh hoạt giải trí R = 40Ω và một tụ điện có điện dung thay đổi được. Giữa AB có một điện áp xoay chiều u = 200cos100πt(V) luôn ổn định. Điều chỉnh C cho tới lúc điện áp hiệu dụng giữa hai đầu mạch MB đạt cực lớn (UMB)Max. Giá trị của (UMB)Max là
A. 361 V. B. 220 V. C. 255 V. D. 281 V.
Giải: công thức $U_RCMtextax=frac2UtextRsqrt4R^2+Z_L^2-Z_L$ -thay những số liệu váo sẽ ra đáp án
Câu 11: Cho mạch điện xoay chiều không phân nhánh có điện trở hoạt động và sinh hoạt giải trí bằng 15Ω, một cuộn cảm thuần có độ tự cảm $fractext2text5 !!pi!!text $H và một tụ điện có điện dung $textC=fractext500text !!pi!!text mu textF$ . Điện áp giữa hai đầu mạch điện là $textu=75sqrttext2textcos100 !!pi!!text t$(V) luôn ổn định. Ghép thêm tụ C’ với C thì điện áp hiệu dụng giữa hai đầu cuộn cảm có mức giá trị lớn số 1 (UL)Max. Giá trị của C’ và (UL)Max lần lượt là
A. $fractext1text0^text-3text !!pi!!text $F; 100V. B. $fractext1text0^text-3text !!pi!!text $F; 200V. C. $fractext1text0^text-3text2 !!pi!!text $F; 200V. D. $fractext1text0^text-3text2 !!pi!!text $F; 100V.
Khi ghép thêm tụ C’ thì ULmax khi $Z_L=Z_cb$=40$Omega $
từ đó suy ra Cb ,thấy rằng Cb
Bài viết gợi ý:Chia Sẻ Link Cập nhật Đặt một điện áp xoay chiều có tần số f thay đổi và giá trị hiệu dụng 30V miễn phí
Bạn vừa tìm hiểu thêm Post Với Một số hướng dẫn một cách rõ ràng hơn về Review Đặt một điện áp xoay chiều có tần số f thay đổi và giá trị hiệu dụng 30V tiên tiến và phát triển nhất và ShareLink Tải Đặt một điện áp xoay chiều có tần số f thay đổi và giá trị hiệu dụng 30V miễn phí.