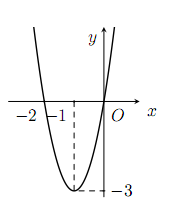Kinh Nghiệm về Trong không khí Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3=0), C(0;0 4) có phương trình 2022
You đang tìm kiếm từ khóa Trong không khí Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3=0), C(0;0 4) có phương trình được Update vào lúc : 2022-03-12 10:23:12 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Trong không khí Oxyz, phương trình mặt phẳng trải qua ba điểm A(0;-1;2), B(-2;0;3)và C(1;2;0)là:
Nội dung chính
- Trong không khí với hệ tọa độ Oxyz , mặt phẳng trải qua 3 điểm A1;2;3 , B4;5;6 , C1;0;2 có phương trình là
- Bài tập trắc nghiệm 60 phút Phương trình mặt phẳng trong không khí – Toán Học 12 – Đề số 10
Trong không khí Oxyz , phương trình mặt phẳng Oyz là
[HH12. C3. 2. D02. b] Trong không khí Oxyz , phương trình mặt phẳng α trải qua M1;3;−2 và tuy nhiên tuy nhiên với mặt phẳng β:2x−y+5z+4=0 là
Trongkhônggianvớihệtọađộ
, chođiểm
vàmặtphẳng
. Phươngtrìnhnàodướiđâylàphươngtrìnhmặtphẳngđi qua
và tuy nhiên songvới
?
Trong không khí với tọa độ Oxyz, cho đường thẳng
và mặt phẳng
. Mặt phẳng (Q.) chứa đường thẳng d và tạo với (P) một góc nhỏ nhất có phương trình.
[Câu 20 – Đề chính thức mã 103 năm 2016-2017] Trong không khí Oxyz, cho điểm M3; −1; −2 và mặt phẳng α:3x−y+2z+4=0. Phương trình nào dưới đấy là phương trình mặt phẳng trải qua M và tuy nhiên tuy nhiên với α ?
Trong không khí với hệ tọa độ Oxyz , cho ba điểm A(2;1;−1), B(−1;0;4), C(0;−2;−1) . Phương trình nào sau này là phương trình của mặt phẳng trải qua A và vuông góc với BC ?
Trong không khí
, cho ba điểm
,
và
. Mặt phẳng
có phương trình là
Trong không khí với hệ tọa độ
cho điểm
.Viết phương trình mặt phẳng
qua E và cắt nửa trục dương
lần lượt tại
sao cho
nhỏ nhất với
là trọng tâm tam giác
.
Trongkhônggianvớihệtọađộ
, chomặtphẳng
cóphươngtrình
Phátbiểunàosauđâylàsai?
Trongkhônggian
,chođiểm
. Gọi
lầnlượtlàhìnhchiếucủa
trêntrục
vàtrênmặtphẳng
. Viếtphươngtrìnhmặttrungtrựccủađoạn
.
Trong không khí với hệ tọa độ
 , cho mặt cầu
, cho mặt cầu  có tâm
có tâm 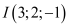 và trải qua điểm
và trải qua điểm 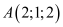 . Mặt phẳng nào dưới đây tiếp xúc với
. Mặt phẳng nào dưới đây tiếp xúc với 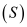 tại
tại 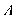 ?
?
Trongkhônggianvớihệ tọađộ Oxyz, chođiểm
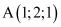 và đườngthẳng
và đườngthẳng. PhươngtrìnhmặtphẳngchứaA và vuônggócvớid là
Trong không khí với tọa độ Oxyz cho đường thẳng
. Viết phương trình mặt phẳng qua điểm
và chứa đường thẳng (d).
Trong không khí với hệ tọa độ
, gọi
là mặt phẳng qua
và cắt những trục
,
,
lần lượt tại những điểm
,
,
(khác gốc
) sao cho
là trọng tâm tam giác
. Khi đó mặt phẳng
có phương trình:
Cho điểm
và đường thẳng
. Mặt phẳng chứa điểm M và đường thẳng d có phương trình là:
Trong không khí với hệ tọa độ Oxyz , mặt phẳng trải qua 3 điểm A1;2;3 , B4;5;6 , C1;0;2 có phương trình là
TrongkhônggianvớihệtrụctọađộOxyz. Viếtphươngtrìnhmặtphẳngđi qua điểm
nhận
làmmộtvectơpháptuyến.
Với
. Phương trình mặt phẳng qua A, B, C là
Trong không khí
 cho ba điểm
cho ba điểm 
 và
và  . Phương trình mặt phẳng
. Phương trình mặt phẳng 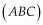 là
là
Cho hai tuyến phố thẳng
và
. Mặt phẳng cách đều hai tuyến phố thẳng
và
có phương trình là
Cho điểm
và đường thẳng
. Mặt phẳng chứa điểm M và đường thẳng d có phương trình là:
TrongkhônggianchoOxyzchomặtphẳng
và haiđiểm
. Phươngtrìnhmặtphẳng
qua A, B vuônggócvới (P) là ?
Trong không khí với hệ tọa độ
 , phương trình nào dưới đấy là phương trình mặt phẳng trải qua điểm
, phương trình nào dưới đấy là phương trình mặt phẳng trải qua điểm và có một vectơ pháp tuyến
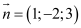 .
.
Trong không khí với hệ tọa độ Oxyz, cho đường thẳng
. Viết phương trình mặt phẳng
trải qua điểm
và vuông góc với d.
Trong không khí Oxyz, cho ba điểm
. Mặt phẳng trải qua Avà vuông góc với đường thẳng BCcó phương trình là
Trong không khí Oxyz , cho điểm A(1;−2;3),B(3;0;−1) . Mặt phẳng trung trực của đoạn
Trongkhônggianvớihệtọađộ
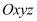 , mặtphẳng
, mặtphẳngnhậnvectơnàosauđâylàmvectơpháptuyến.
Trong không khí với hệ tọa độ
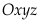 , cho mặt phẳng
, cho mặt phẳng Điểm nào dưới đây thuộc
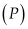 ?
?
Trongkhônggianvớihệtọađộ
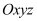 ,mộtvectơpháptuyếncủamặtphẳng
,mộtvectơpháptuyếncủamặtphẳnglà
Trong không khí với hệ tọa độ Oxyz, cho hai mặt phẳng
. Vecto nào dưới đấy là một vecto pháp tuyến của mặt phẳng (P)?
Trong không khí với hệ trục tọa độ
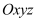 , cho điểm
, cho điểm và hai mặt phẳng
,
. Mặt phẳng
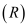 trải qua
trải qua 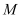 và đồng thời vuông góc với cả hai mặt phẳng
và đồng thời vuông góc với cả hai mặt phẳng có phương trình là
Trong không khí
, mặt phẳng nào sau này nhận
làm vectơ pháp tuyến?
Trong không khí
, cho hai điểm
và
. Mặt phẳng trung trực của
có phương trình là?
Viết phương trình mặt phẳng
trải qua điểm
và tuy nhiên tuy nhiên với mặt phẳng
.
Trong không khí với hệ tọa độ
, gọi
là mặt phẳng qua
và cắt những trục
,
,
lần lượt tại những điểm
,
,
(khác gốc
) sao cho
là trọng tâm tam giác
. Khi đó mặt phẳng
có phương trình?
[ Mức độ 2] Trong không khí
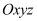 , mặt phẳng trải qua
, mặt phẳng trải qua 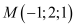 và vuông góc với đường thẳng
và vuông góc với đường thẳng có phương trình là
Trong không khí với hệ trục tọa độ
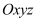 , cho điểm
, cho điểm và hai mặt phẳng
,
. Mặt phẳng
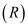 trải qua
trải qua 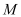 và đồng thời vuông góc với cả hai mặt phẳng
và đồng thời vuông góc với cả hai mặt phẳng có phương trình là
Trongkhônggianvớihệtọađộ
chomặtphẳng
Vectơnàodướiđâylàvectơpháptuyếncủa
TrongkhônggianvớihệtrụctọađộOxyz, chomặtphẳng
. Hỏimặtphẳngnàycógìđặcbiệt?
Mặt phẳng
chứa gốc tọa độ O và vuông góc với 2 mặt phẳng
và
có phương trình là:
Cho hàm số $y=f(x)=ax^3+bx^2+cx+d$ có đạo hàm là hàm số $y=f'(x)$ với đồ thị như hình vẽ dưới đây. Biết rằng đồ thị hàm số $y=f(x)$ tiếp xúc với trục hoành tại điểm có hoành độ âm. Khi đó đồ thị hàm số cắt trục tung tại điểm có tung độ là bao nhiêu?
Một con lắc đơn gồm sợi dây có khối lượng không đáng kể, không dãn, có chiều dài ℓ và viên bi nhỏ có khối lượng m. Kích thích cho con lắc xấp xỉ điều hoà ở nơi có tần suất trọng trường g. Nếu chọn mốc thế năng tại vị trí cân đối của viên bi thì thế năng của con lắc này ở li độ góc α có biểu thức là
Cho hàm số $ y=2x^3-(3m+3)x^2+6mx-4 $ có đồ thị $ left(C_mright) $. Gọi $ T $ là tập những giá trị của tham số $ m $ thỏa mãn nhu cầu $ left(C_mright) $ có đúng hai điểm chung với trục hoành. Tính tổng $ S $ toàn bộ những thành phần của $ T $.
Một con lắc lò xo gồm vật có khối lượng m và lò xo có độ cứng k không đổi, xấp xỉ điều hoà. Nếu khối lượng m = 200 g thì chu kì xấp xỉ của con lắc là 2 s. Để chu kì con lắc là một trong s thì khối lượng m bằng
Biết $A(x_A;y_A)$, $B(x_B;y_B)$ là hai điểm thuộc hai nhánh rất khác nhau của đồ thị hàm số $y=dfracx+1x-1$ sao cho đoạn thẳng $AB$ có độ dài nhỏ nhất. Tính $P=x_A^2+x_B^2+y_Acdot y_B$.
Phát biểu nào sau này là sai khi nói về xấp xỉ cơ học?
Tìm những giá trị của tham số m để đồ thị hàm số: $y = 2 x ^ 3 + 3 ( m – 1 ) x ^ 2 + 6 m ( 1 – 2 m ) x$ có điểm cực lớn và điểm cực tiểu nằm trên đường thẳng có phương trình: $y = – 4 x ( d )$ .
Khi đưa một con lắc đơn lên rất cao theo phương thẳng đứng (coi chiều dài của con lắc không đổi) thì tần số xấp xỉ điều hoà của nó sẽ
Biết đường thẳng $ y=left(3m-1right)x+6m+3$ cắt đồ thị $ y=x^3-3x^2+1$ tại ba điểm phân biệt sao cho có một giao điểm cách đều hai giao điểm còn laị. Khi đó m thuộc khoảng nào dưới đây
Một vật nhỏ xấp xỉ điều hòa có biên độ A, chu kì xấp xỉ T, ở thời gian ban đầu to = 0 vật đang ở vị trí biên. Quãng đường mà vật đi được từ thời gian ban đầu đến thời gian $t = fracT4$ là
Trong không khí (Oxyz), mặt phẳng trải qua 3 điểm (Aleft( 1;0;0 right),,,Bleft( 0;2;0 right),,,Cleft( 0;0;3 right)) có phương trình là:
A.
(dfracx1 + dfracy2 + dfracz3 = 1)
B.
(dfracx1 + dfracy2 + dfracz3 = 0)
C.
(dfracx1 + dfracy2 + dfracz3 = – 1)
D.
(dfracx1 + dfracy1 + dfracz3 = 1)
Trong không khí với hệ trục tọa độ Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3;0), C0;0;4) có phương trình là:
A. 6x + 4y + 3z + 12 = 0
B. 6x + 4y + 3z = 0
C. 6x + 4y + 3z – 12 = 0
D. 6x + 4y + 3z – 24 = 0
Các vướng mắc tương tự
Trong không khí với hệ toạ độ Oxyz, (α) là mặt phẳng trải qua điểm A ( 2 ; – 1 ; 5 ) và vuông góc với hai mặt phẳng ( P ) : 3 x – 2 y + z – 1 = 0 v à ( Q. ) : 5 x – 4 y + 3 z + 10 = 0 . Phương trình mặt phẳng (α) là:
A. x + 2y + z- 5 = 0.
B. 2x – 4y – 2z – 9 = 0.
C. x – 2y + z -1 = 0
D. x- 2y- z + 1 = 0
Trong hệ trục tọa độ Oxyz, cho phương trình mặt phẳng (P): 2x+4y-3z+1=0. Vecto pháp tuyến của (P) là:
A. (2;4;3)
B. (2;4;-3)
C. (2;-4;-3)
D. (-3;4;2)
Trong không khí với hệ tọa độ Oxyz cho hai mặt cầu ( S 1 ) , ( S 2 ) lần lượt có phương trình là x 2 + y 2 + z 2 – 2 x – 2 y – 2 z – 22 = 0 , x 2 + y 2 + z 2 – 6 x + 4 y + 2 z + 5 = 0 . Xét những mặt phẳng (P) thay đổi nhưng luôn tiếp xúc với cả hai mặt cầu đã cho. Gọi M(a;b;c) là yếu tố mà toàn bộ những mp(P) trải qua. Tính tổng S=a+b+c
Trong không khí với hệ trục tọa độ Oxyz, cho điểm A(2;1;3). Mặt phẳng (P) trải qua A và tuy nhiên tuy nhiên với mặt phẳng (Q.): x+2y+3z+2=0 có phương trình là
A. x+2y+3z-9=0
B.x+2y+3z-13=0
C. x+2y+3z+5=0
D. x+2y+3z+13=0
Trong không khí với hệ trục tọa độ Oxyz, cho A ( 3 ; − 1 ; − 3 ) , B ( − 3 ; 0 ; − 1 ) , C ( − 1 ; − 3 ; 1 ) và mặt phẳng ( P ) : 2 x + 4 y + 3 z − 19 = 0 . Tọa độ M ( a , b , c ) thuộc (P) sao cho M A → + 2 M B → + 5 M C → đạt giá trị nhỏ nhất. Khi đó a+b+c bằng:
A. 4
B. 5
C. 6
D. 7
Trong không khí Oxyz. Tính thể tích V của khối đa diện số lượng giới hạn bởi
mặt phẳng (P): 2x – 4y + 3z – 24 = 0 và những mặt phẳng tọa độ.
A. V = 576
B. V= 288
C. V = 192
D. V = 96
Trong không khí với hệ trục tọa độ Oxyz, cho điểm A(2; -1; 0) và mặt phẳng (P): x – 2y – 3z + 10 = 0. Phương trình mặt phẳng (Q.) trải qua A và tuy nhiên tuy nhiên với mặt phẳng (P) là:
A. x – 2y + 3z + 4 = 0
B. -x + 2y + 3z + 4 = 0
C. x – 2y – 3z + 4 = 0
D. x + 2y – 3z = 0.
Trong hệ trục tọa độ Oxyz cho mặt phẳng (P) x-4y+3z-2=0. Một vecto pháp tuyến của (P)
A. (0;-4;3)
B. (1;4;3)
C. (-1;4;-3)
Trong không khí Oxyz, biết mặt phẳng ax+by+cz-24=0 qua A(1;2;3) và vuông góc với hai mặt phẳng (P): 3x-2y+z+4=0, (Q.): 5x-4y+3z+1=0. Giá trị a+b+c bằng
A. 8.
B. 9.
C. 10.
D. 12.
Trong không khí với hệ tọa độ Oxyz , mặt phẳng trải qua 3 điểm A1;2;3 , B4;5;6 , C1;0;2 có phương trình là
A.x−y+2z−5=0 .
B.x+2y−3z+4=0 .
C.3x−3y+z=0 .
D.x+y−2z+3=0 .
Đáp án và lời giải
Đáp án:D
Lời giải:Lời giải
Chọn D
Ta có: AB→=3;3;3 , AC→=0;−2;−1
Mặt phẳng trải qua 3 điểm A1;2;3 , B4;5;6 , C0;1;2 nhận n→=AB→,AC→=3;3;−6 làm véctơ pháp tuyến.
Nên phương trình mặt phẳng trải qua 3 điểm A1;2;3 , B4;5;6 , C1;0;2 có phương trình là 3x+3y−6z+9=0 hay x+y−2z+3=0
Vậy đáp án đúng là D.
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 60 phút Phương trình mặt phẳng trong không khí – Toán Học 12 – Đề số 10
Làm bài
Chia sẻ
Một số vướng mắc khác cùng bài thi.
Một số vướng mắc khác hoàn toàn có thể bạn quan tâm.
Share Link Cập nhật Trong không khí Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3=0), C(0;0 4) có phương trình miễn phí
Bạn vừa tìm hiểu thêm Post Với Một số hướng dẫn một cách rõ ràng hơn về Video Trong không khí Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3=0), C(0;0 4) có phương trình tiên tiến và phát triển nhất và Share Link Cập nhật Trong không khí Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3=0), C(0;0 4) có phương trình Free.

Thảo Luận vướng mắc về Trong không khí Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3=0), C(0;0 4) có phương trình
Nếu sau khi đọc nội dung bài viết Trong không khí Oxyz, mặt phẳng trải qua những điểm A(2;0;0), B(0;3=0), C(0;0 4) có phương trình vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Admin lý giải và hướng dẫn lại nha
#Trong #không #gian #Oxyz #mặt #phẳng #đi #qua #những #điểm #A200 #B030 #C00 #có #phương #trình