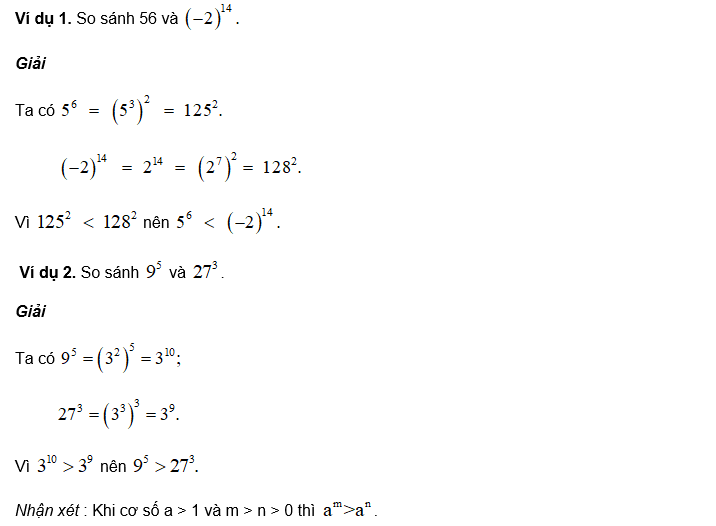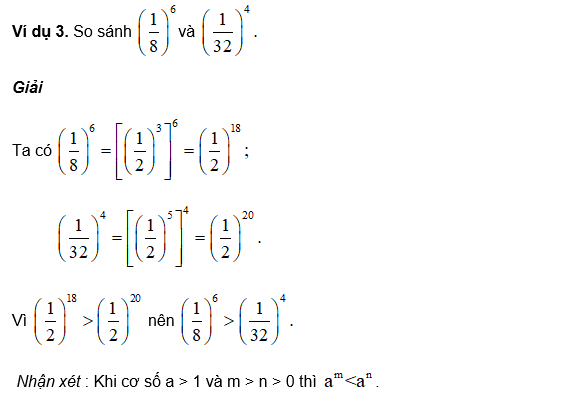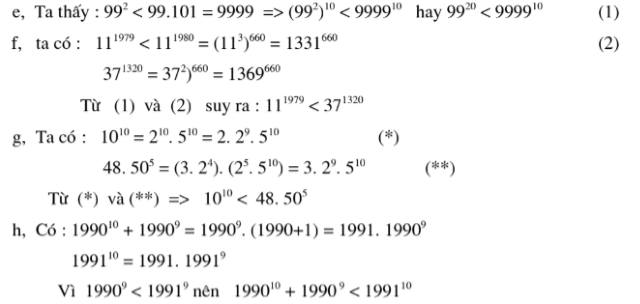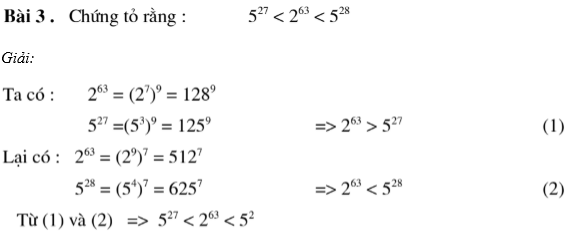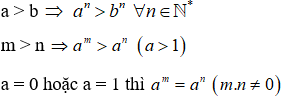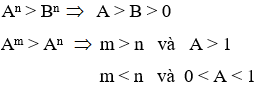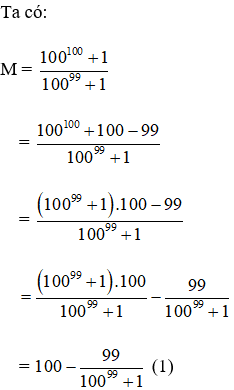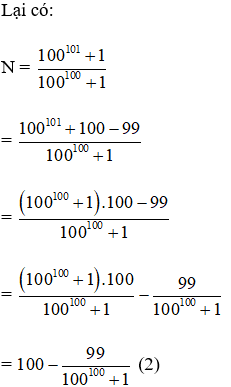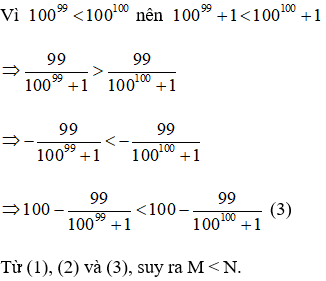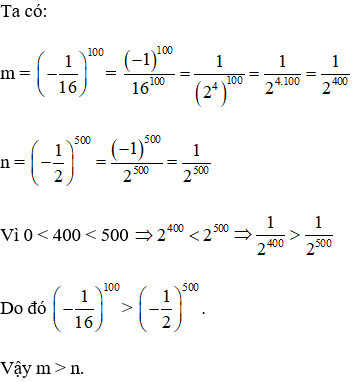Thủ Thuật về Bài toán so sánh lũy thừa lớp 7 2022
You đang tìm kiếm từ khóa Bài toán so sánh lũy thừa lớp 7 được Cập Nhật vào lúc : 2022-03-25 08:44:10 . Với phương châm chia sẻ Mẹo về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi Read Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Admin lý giải và hướng dẫn lại nha.
Phương pháp giải
Nội dung chính
- A. so sánh hai số lũy thừa cùng cơ số :
- B. so sánh hai số lũy thừa cùng số mũ :
- C. so sánh hai số lũy thừa khác cơ số và số mũ :
-
 Tải app VietJack. Xem lời giải nhanh hơn!
Tải app VietJack. Xem lời giải nhanh hơn! - Giải bài tập Toán 7
- Giải SBT Toán 7
- Top 60 Đề thi Toán 7 (có đáp án)
-
 Hỏi bài tập trên ứng dụng, thầy cô VietJack vấn đáp miễn phí!
Hỏi bài tập trên ứng dụng, thầy cô VietJack vấn đáp miễn phí! - Hơn 20.000 câu trắc nghiệm Toán,Văn, Anh lớp 7 có đáp án
Có thể đưa về so sánh hai luỹ thừa cùng số mũ hoặc cùng cơ số.
Related
Cách so sánh lũy thừa lớp 7 nâng cao | dạy bé học toán lớp 6 7 8 9 trực tuyến trực tuyến miễn phí không lấy phí
( so sánh lũy thừa lớp 7, cách so sánh lũy thừa lớp 7, so sánh lũy thừa nâng cao, toán lớp 7 so sánh lũy thừa, so sánh lũy thừa lớp 6 nâng cao, so sánh số hữu tỉ lớp 7 nâng cao
Dạng 3: So sánh hai lũy thừa
*) Phương pháp: để so sánh hai lũy thừa ta thường biến hóa về hai lũy thừa có cùng cơ số hoặc số mũ (hoàn toàn có thể sử dụng lũy thừa trung gian để so sánh).
Lưu ý một số trong những tính chất:
Với (a,,b,,m,,n in N,) ta có:
(beginarrayla,, > ,,b Leftrightarrow a^n,, > ,,b^n,,,,,,,forall n in N^*\m,, > ,,n Leftrightarrow a^m,, > ,,a^n,,,,,left( a,, > ,,1 right)\left[ beginarrayla = 0\a = 1endarray right. Rightarrow a^m = a^n,,,,,,left( m,n ne 0 right)endarray)
Với A, B là những biểu thức ta có:
(beginarraylA^n,, > ,,B^n Leftrightarrow A,, > ,,B,, > ,,0\A^m,, > ,,A^n,, Rightarrow m,, > ,,n,;,,A,, > ,,1\,,,,,,,,,,,,,,,,,,,,,,,,,,,m,, < ,,n,;,,0,, < ,,A,, < 1endarray)
Tất cả nội dung nội dung bài viết. Các em hãy click more và tải file rõ ràng dưới đây:
>> Học trực tuyến lớp 7 trên Tuyensinh247.com cam kết giúp học viên lớp 7 học tốt, hoàn trả học phí nếu học không hiệu suất cao.
10 Th11
–o0o–
A. so sánh hai số lũy thừa cùng cơ số :
với a > 1, n > 0, ta có : n < m nên : an < am
ví dụ : so sánh hai số lũy thừa : 930 và 2720
ta có : 930 = (32)30 = 360
2721 = (33)21 = 363
Do 60 < 63 nên : 360 < 363
Vậy : 930 < 2721
B. so sánh hai số lũy thừa cùng số mũ :
với 1 < a < b , n > 0. ta có : an < bn
ví dụ : so sánh hai số lũy thừa : 2210 và 5140
ta có : 2210 = (23)70 = 870
5140 = (52)70 = 2570
Do 8 < 25 nên : 870 < 2570
Vậy : 2210 < 5140
C. so sánh hai số lũy thừa khác cơ số và số mũ :
tính chất thứ tự (tính bắc cầu) a < b và b < c nên : a < b < c
ví dụ : so sánh hai số lũy thừa : 291 và 535
do 90 < 91 nên : 290 < 291
290 = (25)18 = 3218
Suy ra : 3218 < 291
do 35 < 36 nên : 535 < 536
536 = (22)18 = 2518
Suy ra : 535 < 2518
Do 25 < 32 nên : 2518 < 3218
Vậy : 535< 2518 < 3218 < 291
Hay : 535 < 291
– Một số tính chất:
Với a, b, m, n ∈ N, ta có:
Với A, B là những biểu thức ta có:
– Phương pháp: Để so sánh hai lũy thừa ta thường biến hóa về hai lũy thừa có cùng cơ số rồi so sánh số mũ hoặc đưa về cùng số mũ rồi so sánh cơ số. Ngoài ra hoàn toàn có thể dùng lũy thừa trung gian để so sánh.
Ví dụ 1: So sánh những lũy thừa sau
a) 3317 và 3327
b) 201910 và 202010
Lời giải:
a) 3317 và 3327
Vì 1 < 17 < 27 nên 3317 < 3327 (hai lũy thừa cùng cơ số)
b) 201910 và 202010
Vì 2022 < 2022 nên 201910 < 202010 (hai lũy thừa cùng số mũ)
Ví dụ 2: So sánh hai số (-32)9 và (-16)13
Lời giải:
Ta có: (-32)9 = -329 (Tính chất lũy thừa với số mũ lẻ)
Suy ra (-32)9 = -329 = -(25)9 = -25.9 = -245
Tương tự: (-16)13 = -1613 = -(24)13 = -24.13 = -252
Vì 0 < 45 < 52 ⇒ 245 < 252 ⇒ -245 > -252 (nhân hai vế với -1)
Vậy (-32)9 < (-16)13.
Ví dụ 3: So sánh
a) 2300 và 3200
b) 85 và 3.47
Lời giải:
a) 2300 và 3200
Ta có:
> 2300 = 23.100 = (23)100 = 8100;
> 3200 = 32.100 = (32)100 = 9100
Vì 0 < 8 < 9 nên 8100 < 9100
Vậy 2300 < 3200
b) 85 và 3.47
Ta có:
85 = (23)5 = 23.5 = 215 = 2.214
3.47 = 3.(22)7 = 3.22.7 = 3.214
Vì 2 < 3 nên 2.214 < 3.214 (do 214> 0)
Vậy 85 và 3.47
Câu 1. Điền dấu >; < ; thích hợp vào chỗ trống
a) 321 …… 221
b) 333317 ……… 333323
c) (2022 – 2022)2022 …….. (1998 – 1997)202020
Hiển thị đáp án
Hướng dẫn
a) Vì 3 > 2 > 0 nên 321 > 221 (hai lũy thừa cùng số mũ)
b) Vì 17 < 23 và 3333 > 1 nên 333317 < 333323 (hai lũy thừa cùng cơ số)
c) Ta có:
> (2022 – 2022)2022 = 12020 = 1
> (1998 – 1997)202020 = 1202020 = 1
Vậy (2022 – 2022)2022 = (1998 – 1997)202020
Câu 2. Cho hai số a = 9920 và b = 999910. Khẳng định nào sau này là đúng
A. a = b
B. a < b
C. a > b
D. a ≥ b
Hiển thị đáp án
Hướng dẫn
Ta có:
> a = 9920 = 992.10 = (992)10 = (99.99)10 = 980110
> b = 999910
Vì 0 < 9801 < 9999
Suy ra 980110 < 999910 (hai lũy thừa cùng cơ số)
Do đó 9920 < 999910
Vậy a < b
Đáp án B
Câu 3. Cho hai số a = 111979 và b = 371320. Khẳng định nào sau này đúng?
A. a < b
B. a = b
C. a > b
D. a ≤ b
Hiển thị đáp án
Hướng dẫn
Ta có:
> a = 111979 < 111980 = 113.660 = (113)660 = 1331660
> b = 371320 = 372.660 = (372)660 = 1369660
Vì 0 < 1331 < 1369 nên 1331660 < 1369660
Do đó a = 111979 < 1331660 < 1369660 = 371320 = b
Vậy a < b.
Đáp án A
Câu 4. Cho A = 199110 và B = 199010 + 19909. So sánh A và B
A. A < B.
B. A = B.
C. A > B.
D. A ≤ B
Hiển thị đáp án
Hướng dẫn
Ta có:
> A = 199110 = 19919 + 1
= 19919.1991
> B = 199010 + 19909
= 19909 + 1 + 19909
= 19909.1990 + 19909
= 19909.(1990 + 1)
= 19909.1991
Vì 1991 > 1990 > 0 nên 19919 > 19909
Suy ra 19919.1991 > 19909.1991
Do đó 199110 > 199010 + 19909
Vậy A > B.
Đáp án C
Câu 5. So sánh a = 36000 và b = 93000.
A. a < b
B. a = b
C. a > b
D. a ≤ b
Hiển thị đáp án
Hướng dẫn
Ta có: a = 36000 = 32.3000 = (32)3000 = 93000
b = 93000
Vậy a = b.
Đáp án B
Câu 6. So sánh 202303 và 303202.
A. 202303 > 303202
B. 202303 < 303202
C. 202303 = 303202
D. 202303 ≥ 303202
Hiển thị đáp án
Hướng dẫn
Ta có:
202303 = 2023.101
= (2023)101
= ((2.101)3)101
= (23.1013)101
= (8.101.1012)101
= (808.1012)101
Lại có:
303202 = 3032.101
= (3032)101
= ((3.101)2)101
= (32.1012)101
= (9.1012)101
Vì 808 > 9 > 0 ⇒ 808.1012 > 9.1012 > 0
Do đó (808.1012)101 > (9.1012)101
Vậy 202303 > 303202
Đáp án A
Câu 7. So sánh 1010 và 48.505.
A. 1010 > 48.505
B. 1010 < 48.505
C. 1010 = 48.505
D. 1010 ≥ 48.505
Hiển thị đáp án
Hướng dẫn
Ta có: 1010 = 109.10
Lại có:
48.505 = 16.3.(5.10)5
= 24.3.55.105
= 24.3.54.5.105
= (24.54).105.(3.5)
= (2.5)4.105.15
= 104.105.15
= 104 + 5.15
= 109.15
Vì 10 < 15 nên 109.10 < 109.15
Vậy 1010 < 48.505.
Đáp án B
Câu 8. Cho a = (-5)30 và b = (-3)50. Chọn xác lập đúng.
A. a > b
B. a < b
C. a = b
D. a ≥ b
Hiển thị đáp án
Hướng dẫn
Ta có: a = (-5)30 = 530 (Tính chất lũy thừa với số mũ chẵn)
Suy ra: a = 530 = 53.10 = (53)10 = 12510
Tương tự: b = (-3)50 = 350 = 35.10 = (35)10 = 24310
Vì 0 < 125 < 243 nên 12510 < 24310
Do đó (-5)30 < (-3)50
Vậy a < b.
Đáp án B
Câu 9. So sánh 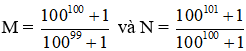
A. M = N
B. M < N
C. M > N
D. M ≤ N
Hiển thị đáp án
Hướng dẫn
Đáp án B
Câu 10. Cho 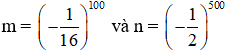
A. m > n
B. m < n
C. m = n
D. m ≥ n
Hiển thị đáp án
Hướng dẫn
Đáp án A
Xem thêm những dạng bài tập Toán lớp 7 tinh lọc, có đáp án hay khác:
Xem thêm những loạt bài Để học tốt Toán 7 hay khác:
Giới thiệu kênh Youtube VietJack
Đã có app VietJack trên điện thoại, giải bài tập SGK, SBT Soạn văn, Văn mẫu, Thi trực tuyến, Bài giảng….miễn phí. Tải ngay ứng dụng trên Android và iOS.
Nhóm học tập facebook miễn phí cho teen 2k9: fb.com/groups/hoctap2k9/
Theo dõi chúng tôi miễn phí trên social facebook và youtube:
Loạt bài Lý thuyết – Bài tập Toán lớp 7 có khá đầy đủ Lý thuyết và những dạng bài có lời giải rõ ràng được biên soạn bám sát nội dung chương trình sgk Đại số 7 và Hình học 7.
Nếu thấy hay, hãy động viên và chia sẻ nhé! Các phản hồi không phù phù thích hợp với nội quy phản hồi website sẽ bị cấm phản hồi vĩnh viễn.
Share Link Download Bài toán so sánh lũy thừa lớp 7 miễn phí
Bạn vừa Read Post Với Một số hướng dẫn một cách rõ ràng hơn về Clip Bài toán so sánh lũy thừa lớp 7 tiên tiến và phát triển nhất và Chia SẻLink Download Bài toán so sánh lũy thừa lớp 7 Free.

Thảo Luận vướng mắc về Bài toán so sánh lũy thừa lớp 7
Nếu sau khi đọc nội dung bài viết Bài toán so sánh lũy thừa lớp 7 vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha
#Bài #toán #sánh #lũy #thừa #lớp