Thủ Thuật về Với 5 chữ số 1;2;3, 4, 5 có the lập được bao nhiêu số gồm 5 chữ số Việt không lặp lại 2022
You đang tìm kiếm từ khóa Với 5 chữ số 1;2;3, 4, 5 có the lập được bao nhiêu số gồm 5 chữ số Việt không lặp lại được Update vào lúc : 2022-02-17 23:23:05 . Với phương châm chia sẻ Thủ Thuật Hướng dẫn trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số rất khác nhau?
A.
A. 120
Nội dung chính
- Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số rất khác nhau?
- Bài tập trắc nghiệm 60 phút Bài toán về hoán vị – TỔ HỢP VÀ XÁC SUẤT – Toán Học 11 – Đề số 7
- Các công thức về tổng hợp
- Bài toán về tạo lập số tự nhiên
- Bài tập vận dụng:
- Bạn cần thêm trợ giúp?
Có 3 viên bi đen rất khác nhau, 4 viên bi đỏ rất khác nhau, 5 viên bi xanh rất khác nhau. Hỏi có bao nhiêu cách sắp xếp những viên bi trên thành một dãy sao cho những viên bi cùng màu ở cạnh nhau?
Từ những chữ số
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên gồm
chữ số đôi một rất khác nhau:
Có 10 vịnguyênthủQuốcgiađượcxếpngồivàomộtdãyghếdàitrongđócóôngTrumvàông Kim. Sốcáchxếpsaochohaivịngàyngồicạnhnhaulà.
Sắp xếp năm bạn học viên An, Bình, Chi, Dũng, Lệ vào một trong những chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng luôn ngồi ở hai đầu ghế?
Có bao nhiêu cách sắp xếp
thí sinh vào một trong những phòng thi có
bàn mỗi bàn một thí sinh.
Từ những số
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên có
chữ số rất khác nhau đôi một?
Tập
có toàn bộ bao nhiêu hoán vị?
Từ những chữ số
;
;
;
hoàn toàn có thể lập được bao nhiêu số tự nhiên có
chữ số đôi một rất khác nhau?
Có bao nhiêu cách sắp xếp
thí sinh vào một trong những phòng thi có
bàn mỗi bàn một thí sinh.
Từ những chữ số
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên gồm
chữ số đôi một rất khác nhau:
Từ các chữ số
,
,
lập. được bao nhiêu số tự nhiên có
chữ số, trong đó chữ số
có mặt
lần, chữ số
có mặt
lần, chữ số
có mặt
lần?
Từ những chữ số
,
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên lẻ có
chữ số rất khác nhau và trong mọi số đó tổng của ba chữ số đầu to nhiều hơn tổng của ba chữ số cuối một cty?
Có bao nhiêu cách sắp xếp chỗ ngồi cho 5 học viên vào 5 ghế xếp thành 1 dãy?
Số cách sắp xếp
học viên ngồi vào một trong những bàn dài có
ghế là:
Giải phương trình
Ta có:
Cho
. Từ
lập được bao nhiêu số tự nhiên có
chữ số đôi một rất khác nhau?
Cho tập hợp
gồm
thành phần. Số những hoán vị của
thành phần của tập hợp
là:
Có bao nhiêu cách sắp xếp
học viên thành một hàng dọc?
Có bao nhiêu cách sắp xếp
học viên thành một hàng dọc?
Cho
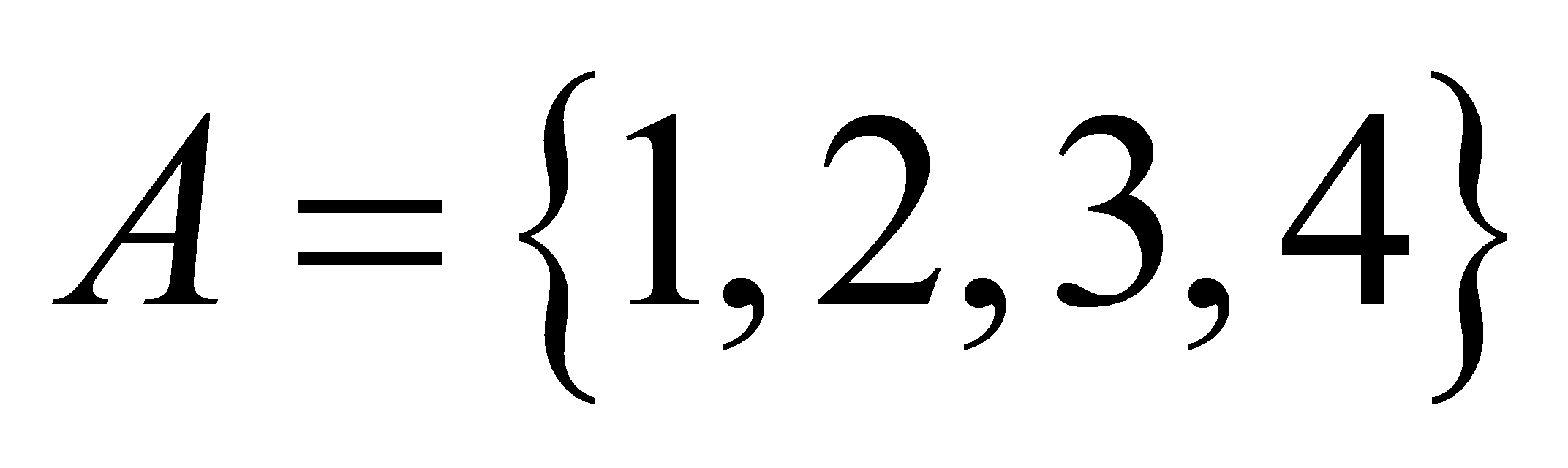. Từ 
lập được bao nhiêu số tự nhiên có 
chữ số đôi một rất khác nhau? Từ những chữ số
,
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên lẻ có
chữ số rất khác nhau và trong mọi số đó tổng của ba chữ số đầu to nhiều hơn tổng của ba chữ số cuối một cty
Có
con mèo vàng,
con mèo đen,
con mèo nâu,
con mèo trắng ,
con mèo xanh và
con mèo tím. Xếp
con mèo thành hàng ngang vào
cái ghế, mỗi ghế một con. Hỏi có bao nhiêu cách sắp xếp chỗ sao cho mèo vàng và mèo đen ở cạnh nhau?
Cho tập hợp
gồm
thành phần. Số những hoán vị của
thành phần của tập hợp
là:
Sắp xếp năm bạn học viên Cường, Hồng, Hoa, Nam, Mai vào một trong những chiếc ghế dài có
chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn Cường và bạn Nam không ngồi cạnh nhau?
Từ những chữ số
, 
, 
, 
, 
, 
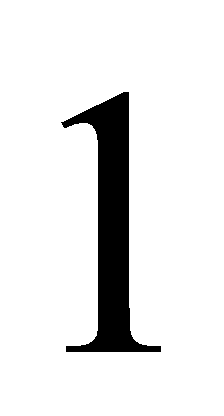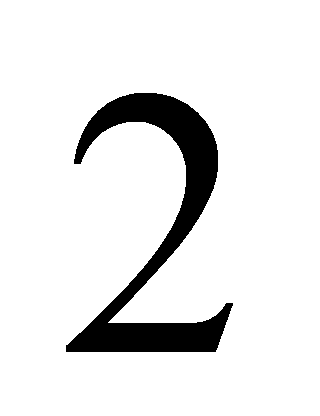hoàn toàn có thể lập được bao nhiêu số tự nhiên lẻ có 
chữ số rất khác nhau và trong mọi số đó tổng của ba chữ số đầu to nhiều hơn tổng của ba chữ số cuối một cty Từ những chữ số
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên gồm
chữ số đôi một rất khác nhau:
Tính tổng của toàn bộ những số có 5 chữ số đôi một rất khác nhau được lập thành từ tập
Cho 5 chữ số 1, 2, 3, 4, 5. Từ 5 chữ số này ta lập được bao nhiêu số tự nhiên có 5 chữ số rất khác nhau?
Từ những chữ số
;
;
hoàn toàn có thể lập được bao nhiêu số tự nhiên có
chữ số rất khác nhau đôi một?
Sắp xếp năm bạn học viên An, Bình, Chi, Dũng, Lệ vào một trong những chiếc ghế dài có 5 chỗ ngồi. Hỏi có bao nhiêu cách sắp xếp sao cho bạn An và bạn Dũng luôn ngồi ở hai đầu ghế?
Có bao nhiêu số tự nhiên ba chữ số đôi một rất khác nhau mà tổng chữ số đầu và cuối bằng
?
Có
con mèo vàng,
con mèo đen,
con mèo nâu,
con mèo trắng ,
con mèo xanh và
con mèo tím. Xếp
con mèo thành hàng ngang vào
cái ghế, mỗi ghế một con. Hỏi có bao nhiêu cách sắp xếp chỗ sao cho mèo vàng và mèo đen ở cạnh nhau?
Một nhóm học viên gồm
học viên nam và
học viên nữ. Hỏi có bao nhiêu cách sắp xếp
học viên trên thành
hàng dọc sao cho nam nữ đứng xen kẽ?
Một tổ có 6 học viên, trong số đó có 3 học viên nam và 3 học viên nữ. Hỏi có bao nhiêu cách xếp những học viên trong tổ thành một hàng dọc sao cho nam, nữ đứng xen kẽ nhau?
Từ những chữ số
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên gồm
chữ số đôi một rất khác nhau:
Có toàn bộ bao nhiêu cách xếp 6 quyển sách rất khác nhau vào một trong những hàng ngang trên giá sách?
Tính tổng của toàn bộ những số có 5 chữ số đôi một rất khác nhau được lập thành từ tập
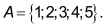
Có bao nhiêu cách sắp xếp
học viên thành một hàng dọc?
Biếu thức:
bằng:
Công thức tính số hoán vị
là:
Cho hàm sô
. Gọi S làtập hợp những giátrịnguyên của
đểhàm sốxác định trên
. Hỏi tập S cóbao nhiêu thành phần?
Miền nghiệm của bất phương trình:
là:
Trong số những tác nhân tự nhiên, tác nhân nào dưới đây đóng vai trò quan trọng nhất riêng với việc phân loại của những thảm thực vật trên toàn thế giới?
Trong những đẳng thức sau, đẳng thức nào đúng?
Trong những mệnh đề sau, mệnh đề nào sai?
Viết phương trình tiếp tuyến của đồ thị hàm số y=−x2+5 tại điểm có tung độ bằng −1 và hoành độ âm.
Phương pháp chấm điểm được sử dụng để thể hiện những đối tượng người dùng địa lý và điểm lưu ý
Nguồn lực nào sau này là nguồn lực về vị trí địa lí:
Thuật toán có tính:
Phương trình lượng giác:
có nghiệm là:
B.
B. 60
C.
C. 30
D.
D. 40
Đáp án và lời giải
Đáp án:A
Lời giải:
Chọn đáp án A
Số có 5 chữ số rất khác nhau dc tạo thành từ tập trên là 5! = 120.
Đáp. án đúng là A
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 60 phút Bài toán về hoán vị – TỔ HỢP VÀ XÁC SUẤT – Toán Học 11 – Đề số 7
Làm bài
Chia sẻ
Một số vướng mắc khác cùng bài thi.
Một số vướng mắc khác hoàn toàn có thể bạn quan tâm.
Các công thức về tổng hợp
Trong Toán học, tổng hợp là cách chọn những thành phần từ một nhóm to nhiều hơn mà không phân biệt thứ tự. Trong những trường hợp nhỏ hơn hoàn toàn có thể đếm được số tổng hợp. Ví dụ cho ba loại quả, một quả táo, một quả cam và một quả lê, có ba cách phối hợp hai loại quả từ tập hợp này: một quả táo và một quả lê; một quả táo và một quả cam; một quả lê và một quả cam.
1. Tổ hợp không lặp
Cho tậpAgồmnphần tử. Mỗi tập con gồmk (1≤ k ≤ n)thành phần củaAđược gọi là một tổng hợp chập k của n thành phần.
Theo định nghĩa, tổng hợp chập k của n thành phần là một tập con của tập hợp mẹ S chứa n thành phần, tập con gồm k thành phần riêng không liên quan gì đến nhau thuộc S và không sắp thứ tự. Số tổng hợp chập k của n thành phần bằng với thông số nhị thức.
Tổ hợp chập k của n thành phần là số những nhóm gồm k thành phần được lấy ra từ n thành phần mà giữa chúng chỉ rất khác nhau về thành phần cấu trúc chứ không quan trọng về thứ tự sắp xếp những thành phần. Các nhóm sẽ là giống nhau nếu chúng có chung thành phần cấu trúc. VD: 1;2;3 và 2;1;3 là giống nhau.
2. Tổ hợp lặp
Cho tậpA = a1; a2; ….; anvà số tự nhiên k bất kỳ. Một tổng hợp lặp chập k của n thành phần là một tập hợp gồm k thành phần, trong số đó, mỗi thành phần là một trong n thành phần của A.
Bài toán về tạo lập số tự nhiên
Các bài tập về lập số những số tự nhiên thường ta vị trí căn cứ vào cấu trúc số tự nhiên để lập những số theo yêu cầu của đề bài. Nên để ý quan tâm lập số theo một thứ tự nhất định, như: từ nhỏ đến lớn hoặc ngược lại từ lớn đến nhỏ như vậy sẽ ít bị sai sót hơn.
CÁCH 1: Liệt kê
Ví dụ 1: Cho 3 chữ số 1; 2; 3. Lập được toàn bộ bao nhiêu số tự nhiên có 3 chữ số?
Bài giải:
Các số tự nhiên có 3 chữ số được viết từ 3 chữ số: 1; 2; 3 là:
111; 112; 113; 121; 122; 123; 131; 132; 133
211; 212; 213; 221; 222; 223; 231; 232; 233
311; 312; 313; 321; 322; 323; 331; 332; 333
Có toàn bộ 27 số.
Ví dụ 2: Cho 3 chữ số 1; 2; 3. Lập được toàn bộ bao nhiêu số tự nhiên có 3 chữ số rất khác nhau?
Bài giải:
Các số tự nhiên có 3 chữ số rất khác nhau được viết từ 3 chữ số: 1; 2; 3 là:
123; 132; 213; 231; 312; 321.
Có toàn bộ 6 số.
Ví dụ 3: Cho 4 chữ số 0; 1; 2; 3. Lập được toàn bộ bao nhiêu số tự nhiên có 3 chữ số rất khác nhau?
Bài giải:
Các số tự nhiên có 3 chữ số rất khác nhau được viết từ 4 chữ số: 0; 1; 2; 3 là:
102; 103; 120; 123; 130; 132
201; 203; 210; 213; 230; 231
301; 302; 310; 312; 320; 321
Có toàn bộ 18 số.
CÁCH 2:
Qua 3 ví dụ trên, ta thấy ở bài tập nêu ra có số lượng chữ số cho trước gồm những chữ số rõ ràng và yêu cầu của số cần lập là ra làm sao? Ta có cách tìm số lượng những số được lập mà tránh việc phải liệt kê, như sau:
Ví dụ 1: Cho 3 chữ số 1; 2; 3. Lập được toàn bộ bao nhiêu số tự nhiên có 3 chữ số?
Ở bài tập này đề bài cho ta 3 chữ số là một trong; 2; 3. Yêu cầu ta lập những số có 3 chữ số mà số có 3 chữ số gồm có: hàng trăm, hàng trăm và hàng cty.
Bài giải:
Với 3 chữ số: 1; 2; 3.
– Hàng trăm có 3 lựa chọn.
– Hàng chục có 3 lựa chọn.
– Hàng cty có 3 lựa chọn.
Số lượng số có 3 chữ số lập được là: 3 x 3 x 3 = 27 (số)
Ví dụ 2: Cho 3 chữ số 1; 2; 3. Lập được toàn bộ bao nhiêu số tự nhiên có 3 chữ số rất khác nhau?
Ở bài này khác với bài 1 là lập số có 3 chữ số rất khác nhau nên nếu đã chọn hàng trăm rồi thì không được chọn ở hàng trăm và hàng cty.
Bài giải:
Với 3 chữ số: 1; 2; 3.
– Hàng trăm có 3 lựa chọn.
– Hàng chục có 2 lựa chọn.
– Hàng cty có một lựa chọn.
Số lượng số có 3 chữ số lập được là: 3 x 2 x 1 = 6 (số)
Ví dụ 3: Cho 4 chữ số 0; 1; 2; 3. Lập được toàn bộ bao nhiêu số tự nhiên có 3 chữ số rất khác nhau?
Ở bài này, những số cho trước có chữ số 0. Chữ số 0 không được đặt tại hàng cao nhất với số tự nhiên (số có 3 chữ số không thể là 023).
Bài giải:
Với 4 chữ số: 0; 1; 2; 3.
– Hàng trăm có 3 lựa chọn. (không được chọn chữ số 0).
– Hàng chục có 3 lựa chọn.
– Hàng cty có 2 lựa chọn.
Số lượng số có 3 chữ số lập được là: 3 x 3 x 2 = 18 (số)
CÁCH 3: Sơ đồ HÌNH CÂY
Lập sơ đồ HÌNH CÂY đó đó là rõ ràng của cách 2 giúp học viên hiểu và liệt kê ra những số một cách tương đối đúng chuẩn hơn, dễ kiểm tra và tránh khỏi những sai sót khi lập số.
Ví dụ 1: Cho 3 chữ số 1; 2; 3. Lập được toàn bộ bao nhiêu số tự nhiên có 3 chữ số?
Ở bài này ta lập sơ đồ như sau:
………..
Bài tập vận dụng:
Bài toán 1: Cho 3 chữ số 5, 6, 8. Hãy lập toàn bộ những số có hai chữ số rất khác nhau từ 3 chữ số trên. Có toàn bộ bao nhiêu số như vậy?
Giải: Lần lượt đặt những chữ số 5, 6, 8 vào hàng trăm ta được những số sau:
56, 58, 65, 68, 85, 86
Có toàn bộ 6 số như vậy.
Bài toán 2: Cho 3 chữ số 2, 4, 6.
a. Hãy lập những số có 3 chữ số từ những chữ số trên.
b. Hãy lập những số có 3 chữ số rất khác nhau từ những số trên.
Giải:
a. Các số được lập phải thỏa mãn nhu cầu những Đk:
Có 3 chữ số; được lập từ những chữ số đã cho; trong mọi số những chữ số hoàn toàn có thể lặp lại.
b. Các số được lập phải thỏa mãn nhu cầu những Đk:
Có 3 chữ số; được lập từ những chữ số đã cho; trong mọi số những chữ số không lặp lại.
Bài toán 3: Cho 5 chữ số 1, 2, 3, 4, 5 em viết được bao nhiêu số:
a. Có 3 chữ số
b. Có 3 chữ số rất khác nhau?
Giải:
a. Có 5 cách chọn chữ số hàng trăm (là một trong năm chữ số 1, 2, 3, 4, 5). Với mỗi cách chọn chữ số hàng trăm thì có 5 cách chọn chữ số hàng trăm. Với mỗi cách chọn chữ số hàng trăm thì có 5 cách chọn chữ số hàng cty.
Vậy số lượng số có 3 chữ số thỏa mãn nhu cầu bài toán là:
5 x 5 x 5 = 125 (số)
b. Với năm chữ số 1, 2, 3, 4, 5 ta có 5 cách chọn chữ số hàng trăm. Với mỗi cách chọn chữ số ở hàng trăm thì chỉ có 4 cách chọn chữ số ở hàng trăm (là một trong bốn chữ số còn sót lại). Với mỗi cách chọn chữ số ở hàng trăm thì chỉ từ 3 cách chọn chữ số ở hàng cty.
Vậy số lượng số có 3 chữ số thỏa mãn nhu cầu bài toán là:
5 x 4 x 3 = 60 (số)
Đáp số: a, 125 số
b, 60 số
Bài toán 4: Cho 5 chữ số 0, 1, 2, 3, 4 em viết được bao nhiêu số có 3 chữ số rất khác nhau?
Giải: Ta có 4 cách chọn chữ số ở hàng trăm là một trong bốn chữ số khác 0: 1, 2, 3, 4. Sau khi đã chọn chữ số ở hàng trăm ta có 4 cách chọn chữ số ở hàng trăm là một trong bốn chữ số còn sót lại. sau khi đã chọn chữ số ở hàng trăm, hàng trăm rồi thì chỉ từ 3 cách chọn chữ số ở hàng cty.
Vậy số lượng số có 3 chữ số thỏa mãn nhu cầu bài toán là:
4 x 4 x 3 = 48 (số)
Đáp số: 48 số
…………………………….
Bạn cần thêm trợ giúp?
Bạn luôn hoàn toàn có thể hỏi một Chuyên Viên trong Cộng đồng Kỹ thuật Excel hoặc nhận sự tương hỗ trongCộng đồng vấn đáp.
Xem thêm
Định dạng số dưới dạng tiền tệ trong Excel
Định dạng số
Reply
6
0
Chia sẻ
Share Link Download Với 5 chữ số 1;2;3, 4, 5 có the lập được bao nhiêu số gồm 5 chữ số Việt không lặp lại miễn phí
Bạn vừa Read Post Với Một số hướng dẫn một cách rõ ràng hơn về Review Với 5 chữ số 1;2;3, 4, 5 có the lập được bao nhiêu số gồm 5 chữ số Việt không lặp lại tiên tiến và phát triển nhất và Share Link Down Với 5 chữ số 1;2;3, 4, 5 có the lập được bao nhiêu số gồm 5 chữ số Việt không lặp lại Free.
Hỏi đáp vướng mắc về Với 5 chữ số 1;2;3, 4, 5 có the lập được bao nhiêu số gồm 5 chữ số Việt không lặp lại
Nếu sau khi đọc nội dung bài viết Với 5 chữ số 1;2;3, 4, 5 có the lập được bao nhiêu số gồm 5 chữ số Việt không lặp lại vẫn chưa hiểu thì hoàn toàn có thể lại phản hồi ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Với #chữ #số #có #lập #được #bao #nhiêu #số #gồm #chữ #số #Việt #không #lặp #lại