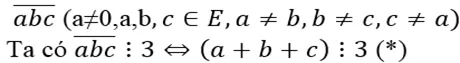Thủ Thuật Hướng dẫn Từ 0 1 2 3 4, 5 lập được bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 5 Mới Nhất
You đang tìm kiếm từ khóa Từ 0 1 2 3 4, 5 lập được bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 5 được Update vào lúc : 2022-02-06 23:35:05 . Với phương châm chia sẻ Mẹo Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi tìm hiểu thêm Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Các công thức về tổng hợp
Trong Toán học, tổng hợp là cách chọn những thành phần từ một nhóm to nhiều hơn mà không phân biệt thứ tự. Trong những trường hợp nhỏ hơn hoàn toàn có thể đếm được số tổng hợp. Ví dụ cho ba loại quả, một quả táo, một quả cam và một quả lê, có ba cách phối hợp hai loại quả từ tập hợp này: một quả táo và một quả lê; một quả táo và một quả cam; một quả lê và một quả cam.
Nội dung chính
- Các công thức về tổng hợp
- Từ những chữ số 0, 1, 2, 3, 4, 5 ta lập được bao nhiêu số có 3 chữ số đôi một rất khác nhau chia hết cho 5?
- Bài tập trắc nghiệm 60 phút Bài toán dùng quy tắc đếm, cộng và nhân – Toán Học 11 – Đề số 5
- Chương 2: Tổ Hợp – Xác Suất Từ những số 0,1,2,3,4,5 hoàn toàn có thể lập được: Ba…
- 2 Câu vấn đáp
- Câu vấn đáp của bạn
- Câu hỏi liên quan
Gọi
là tập những số tự nhiên có
chữ số đôi một rất khác nhau. Chọn ngẫu nhiên một số trong những thuộc
. Tính xác suất để số được chọn chia hết cho
.
Trong một buổi giao lưu, có 5 học viên trường X và 5 học viên trường Y ngồi vào 2 bàn trái chiều nhau. Hỏi có bao nhiêu cách xếp sao cho 2 người ngồi trái chiều và ngồi cạnh thì khác trường nhau.
Giả sử bạn muốn mua một áo sơ mi cỡ
hoặc cỡ
Áo cỡ
có
màu rất khác nhau, áo cỡ
có
màu rất khác nhau. Hỏi có bao nhiêu sự lựa chọn (về màu áo và cỡ áo)?
Tìm thông số
trong khai triển
Một tổ công nhân có
người. Cần chọn
người, một người làm tổ trưởng, một tổ phó và một thành viên. Hỏi có bao nhiêu cách chọn?
Có bao nhiêu số tự nhiên có 3 chữ số
cho a, b, c là độ dài 3 cạnh của một tam giác cân.
Có
con phố đi từ thành phố A đến thành phố B và có
con phố đi từ thành phố B đến thành phố C (như sơ đồ hình bên). Hỏi ông Phương có bao nhiêu phương pháp để đi từ thành phố A đến thành phố C rồi về lại A mà không còn con phố nào được đi quá một lần và khi đi và về thì chỉ qua B đúng một lần.
Cho tập hợp
. Có thể lập bao nhiêu số gồm 3 chữ số rất khác nhau được xây dựng từ những chữ số thuộc A?
Có bao nhiêu chữ số có 5 chữ số rất khác nhau chia hết cho 5 mà trong màn biểu diễn thập phân của nó không còn những chữ số 7, 8, 9?
Cho tập hợp
và những số
. Hỏi có bao nhiêu số tự nhiên có dạng
sao cho
và
.
Có bao nhiêu số có
chữ số đôi một rất khác nhau hoàn toàn có thể lập được từ những chữ số
,
,
,
,
?
Từ những chữ số 0, 1, 2, 3, 4, 5 hoàn toàn có thể lập được bao nhiêu số có bốn chữ số chia hết cho 15. Kết quả cần tìm là:
Một hộp có chứa 8 bóng đèn red color và 5 bóng đèn màu xanh. Số cách chọn được một bóng đèn trong hộp đó là:
Có bao nhiêu số tự nhiên có
chữ số dạng
thỏa
,
,
là độ dài
cạnh của một tam giác cân ( kể cả tam giác đều )?
Xếp ngẫu nhiên 4 học viên gồm 2 nam và 2 nữ vào hai dãy ghế ngồi trái chiều nhau, mỗi dãy có 2 ghế. Tính xác suất P để 2 học viên nam ngồi vào cùng một dãy ghế.
Từ những chữ số
lập được bao nhiêu số tự nhiên gồm hai chữ số?
Cho những chữ số
,
,
,
,
,
. Từ những chữ số đã cho lập được bao nhiêu số tự nhiên chẵn có
chữ số và những chữ số đôi một bất kỳ rất khác nhau.
Từ những chữ số
,
,
,
,
,
hoàn toàn có thể lập được bao nhiêu số tự nhiên lẻ có bốn chữ số đôi một rất khác nhau và phải xuất hiện chữ số
.
Đi vào một trong những Khu di tích lịch sử lịch sử nọ có bốn cửa Đông, Tây, Nam, Bắc. Một người đi vào tham quan rồi đi ra phải đi hai cửa rất khác nhau. Số cách đi vào và đi ra của người đó là:
Có bao nhiêu số tự nhiên có ba chữ số dạng
với
,
,
sao cho
.
] Biết rằng hàm số
liên tục và với mọi
thì
hoàn toàn có thể nhận một trong những giá trị:
. Hỏi có toàn bộ bao nhiêu hàm số rất khác nhau thỏa mãn nhu cầu đề bài? (Hai hàm số
được gọi là rất khác nhau nếu có
mà
).
Từ thành phố
tới thành phố
có
con phố, từ thành phố
tới thành phố
có
con phố. Hỏi có bao nhiêu cách đi từ
tới
qua
?
Từ những chữ số 0, 1, 2, 3, 4, 5 ta lập được bao nhiêu số có 3 chữ số đôi một rất khác nhau chia hết cho 5?
Gọi
là tập hợp toàn bộ những số tự nhiên gồm 5 chữ số đôi một rất khác nhau được lập từ những chữ số
Tính tổng toàn bộ những số thuộc tâp
Từ những chữ số thuộc tập hợp
có bao nhiêu số có chín chữ số rất khác nhau sao cho chữ số
đứng trước chữ số
, chữ số
đứng trước chữ số
và chữ số
đứng trước chữ số
?
Từ những chữ số 0, 1, 2, 3, 4, 5, 6, 7, 8, 9 hoàn toàn có thể lập được bao nhiêu số có bốn chữ số chia hết cho 25. Kết quả cần tìm là:
Lớp
có
bạn nữ, lớp
có
bạn nam. Có bao nhiêu cách chọn một bạn nữ lớp
và một bạn nam lớp
để dẫn chương trình hoạt động và sinh hoạt giải trí ngoại khóa?
Biển số xe máy của tỉnh
(nếu không kể mã số tỉnh) có
kí tự, trong số đó kí tự ở vị trí thứ nhất là một vần âm (trong bảng
cái tiếng Anh), kí tự ở vị trí thứ hai là một chữ số thuộc tập
mỗi kí tự ở bốn vị trí tiếp theo là một chữ số thuộc tập
Hỏi nếu chỉ dùng một mã số tỉnh thì tỉnh
hoàn toàn có thể làm được nhiều nhất bao nhiêu biển số xe máy rất khác nhau?
Trong một trường THPT, khối
có
học viên nam và
học viên nữ. Nhà trường cần chọn hai học viên trong số đó có một nam và một nữ đi dự trại hè của học viên thành phố. Hỏi nhà trường có bao nhiêu cách chọn?
Một lớp học có 18 học viên nam và 20 học viên nữ. Nếu muốn chọn một học viên nam và một học viên nữ đi dự một cuộc thi nào đó thì số cách chọn là:
Lấy ngẫu nhiên một số trong những tự nhiên có
chữ số.Xác suất để chọn được số tự nhiên có dạng
mà
bằng:
Từ những chữ số 1, 2, 3, 4, 5, 6 hoàn toàn có thể lập được bao nhiêu số có bốn chữ số và chia hết cho 4? Kết quả cần tìm là:
Số 283618125 có bao nhiêu ước số tự nhiên:
Có bao nhiêu số tự nhiên có
chữ số trong số đó những chữ số ở vị trí cách đều chữ số đứng ở chính giữa thì giống nhau?
Có 7 nam 5 nữ xếp thành một hàng ngang. Hỏi có bao nhiêu cách xếp sao cho 2 vị trí đầu và cuối là nam và không còn 2 nữ nào đứng cạnh nhau?
Một người dân có 4 cái quần, 6 cái áo, 3 chiếc cà vạt. Để chọn mỗi thứ một món thì có bao nhiều cách thức chọn bộ
quần-áo-cà vạt
rất khác nhau?
Từ những chữ số 0, 1, 2, 3, 4, 5, 6, 7 hoàn toàn có thể lập được bao nhiêu số có ba chữ số rất khác nhau chứa chữ số 2 và chia hết cho 5?
Giả sử từ tỉnh
đến tỉnh
hoàn toàn có thể đi bằng những phương tiện đi lại: xe hơi, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có
chuyến xe hơi,
chuyến tàu hỏa,
chuyến tàu thủy và
chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh
đến tỉnh
?
Từ những chữ số thuộc tập hợp
có bao nhiêu số có chín chữ số rất khác nhau sao cho chữ số
đứng trước chữ số
, chữ số
đứng trước chữ số
và chữ số
đứng trước chữ số
?
Giả sử từ tỉnh
đến tỉnh
hoàn toàn có thể đi bằng những phương tiện đi lại: xe hơi, tàu hỏa, tàu thủy hoặc máy bay. Mỗi ngày có
chuyến xe hơi,
chuyến tàu hỏa,
chuyến tàu thủy và
chuyến máy bay. Hỏi có bao nhiêu cách đi từ tỉnh
đến tỉnh
?
Xét những ví dụ sau:
Cừu hoàn toàn có thể giao phối với dê tạo thành hợp tử nhưng hợp tử bị chết mà không tăng trưởng thành phôi
Lừa giao phối với ngựa sinh ra con la, con la không hoàn toàn có thể sinh sản
Các cây khác loài có mùa ra hoa rất khác nhau nên hạt phấn của loài cây này sẽ không còn thụ phấn cho hoa của loài cây khác
Các loài ếch nhái sinh sản cùng một mùa nhưng có tập tính giao phối rất khác nhau nên giữa chúng thường không còn sự sinh sản
Có bao nhiêu ví dụ về kiểu cách li sau hợp tử
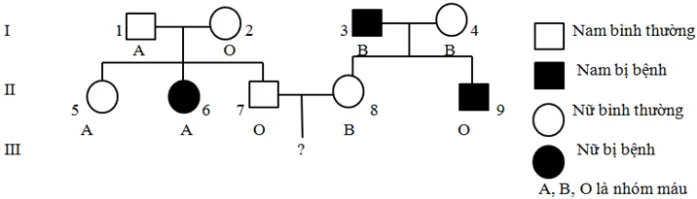
Sơ đồ phả hệ mô tả sự di truyền nhóm máu: A, B,AB, O và một loại bệnh ở người. Biết rằng gen quy đình nhóm máu gồm 3 alen IA; IBvà IO; trong số đó alen IAquy định nhóm máu A; alen IBquy định nhóm máu B đều trội hoàn toàn so với alen IOquy định nhóm máu O và bệnh trong phả hệ là vì một trong 2 alen của một gen quy định trong số đó alen trội là trội hoàn toàn.
Giả sử những cặp gen quy định nhóm máu và những cặp gen quy định bệnh phân li độc lập và không còn đột biến xẩy ra. Trong những kết luận sau ,có bao nhiêu kết luận đúng ?
(1) Có 6 người trong phả hệ này xác lập đúng chuẩn được kiểu gen
(2) Xác suất cặp vợ chồng 7,8 sinh con gái đầu lòng không mang gen bệnh là
(3) Tất cả những người dân bị bệnh trong phả hệ này đều phải có kiểu gen dị hợp tử
(4) Nếu người số 6 kết hôn với những người số 9 thì hoàn toàn có thể sinh ra người con mang nhóm máu ABPhát biểu nào sau này là sai theo mẫu nguyên tử Bo?
Trong không khí Oxyz, cho ba điểm
. Mặt phẳng trải qua Avà vuông góc với đường thẳng BCcó phương trình là
Một gen có chiều dài 408nm. Trong quy trình dịch mã đã tổng hợp nên 1 chuỗi polipeptit có 320 axit amin. Đây là gen của nhóm sinh vật nào ?
Một tia sáng đơn sắc có bước sóng trong chân không là 0,66μm , trong thủy tinh là 0,44μm . Biết rằng vận tốc ánh sáng trong chân không bằng 3. 108 m/s. Tốc độ truyền của tia sáng đơn sắc này trong thủy tinh là
Tìm số câu sai:
1. Quần xã có độ phong phú cao thì số loài nhiều và số lượng thành viên của mỗi loài ít
2. Quần xã ổn định thì số loài nhiều và số lượng thành viên của mỗi loài ít
3. 3.Lưới thức ăn phức tạp dần từ vùng khơi tới ven bờ
4.Sinh vật phân giải hoàn toàn có thể là giun , sâu bọ
5.Một chuỗi thức ăn ở dưới nước có tầm khoảng chừng 4-5 mắt xích
6.Khiđánh bắt nhiều mẻ cá mà thấy cá bé nhiều hơn nữa cá lớn chứng tỏ tài nguyên cá khai thác chưa hết tiềm năng.
Trong việc truyền tải điện năng ra đi, để giảm hiệu suất tiêu tốn trên đường dây n lần thì nên phải
Cho hàm số
(C). Trên (C) lấy điểm A có
. Có bao nhiêu giá trị của m để tiếp tuyến tại A tuy nhiên tuy nhiên với đường thẳng (d) y = 14x – 5.
Trong không khí với hệtoạđộ
,cho hai mặt phẳng
:
;
:
. Giao tuyến của hai mặt phẳng
,
là một đường thẳng trải qua điểm nào dưới đây?
1. Tổ hợp không lặp
Cho tậpAgồmnphần tử. Mỗi tập con gồmk (1≤ k ≤ n)thành phần củaAđược gọi là một tổng hợp chập k của n thành phần.
Theo định nghĩa, tổng hợp chập k của n thành phần là một tập con của tập hợp mẹ S chứa n thành phần, tập con gồm k thành phần riêng không liên quan gì đến nhau thuộc S và không sắp thứ tự. Số tổng hợp chập k của n thành phần bằng với thông số nhị thức.
Tổ hợp chập k của n thành phần là số những nhóm gồm k thành phần được lấy ra từ n thành phần mà giữa chúng chỉ rất khác nhau về thành phần cấu trúc chứ không quan trọng về thứ tự sắp xếp những thành phần. Các nhóm sẽ là giống nhau nếu chúng có chung thành phần cấu trúc. VD: 1;2;3 và 2;1;3 là giống nhau.
Công thức của tổng hợp không lặp
2. Tổ hợp lặp
Cho tậpA = a1; a2; ….; anvà số tự nhiên k bất kỳ. Một tổng hợp lặp chập k của n thành phần là một tập hợp gồm k thành phần, trong số đó, mỗi thành phần là một trong n thành phần của A.
Công thức của tổng hợp lặp
Từ những chữ số 0, 1, 2, 3, 4, 5 ta lập được bao nhiêu số có 3 chữ số đôi một rất khác nhau chia hết cho 5?
A.
A. 12
B.
B. 24
C.
C. 36
D.
D. 48
Đáp án và lời giải
Đáp án:C
Lời giải:
Chọn đáp án C
Trường hợp 1: Số đó có dạng chọn
có
cách nên có
số thỏa mãn nhu cầu Trường hợp 2: Số đó có dạng
chọn
có 4 cách, chọn
có 4 cách nên có 4.4 số thỏa mãn nhu cầu Do đó có
số thỏa mãn nhu cầu.
Đáp. án đúng là C
Câu hỏi thuộc đề thi sau. Bạn có mong ước thi thử?
Bài tập trắc nghiệm 60 phút Bài toán dùng quy tắc đếm, cộng và nhân – Toán Học 11 – Đề số 5
Làm bài
Chia sẻ
Một số vướng mắc khác cùng bài thi.
Một số vướng mắc khác hoàn toàn có thể bạn quan tâm.
Chương 2: Tổ Hợp – Xác Suất Từ những số 0,1,2,3,4,5 hoàn toàn có thể lập được: Ba…
1Chương 2: Tổ Hợp – Xác Suất
Từ những số 0,1,2,3,4,5 hoàn toàn có thể lập được:
Bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 3?
A. 36 B. 42
C. 82944 D. Một kết quả khác

Gửi 3 năm trước đó
Toán lớp 11
2 Câu vấn đáp
Mới nhấtCũ nhấtPhiếu bầu1Sai r b ơi?
Gửi 1 năm trước đó
Thêm bình luận0
Số tự nhiên có ba chữ số rất khác nhau có dạng
Trong E có những bộ chữ số thoả mãn (*) là:
(0,1,2);(0,1,5);(0,2,4);(1,2,3);(1,3,5);(2,3,4);(3,4,5)
Mỗi bộ gồm ba chữ số rất khác nhau và khác 0 nên ta viết được 3*2*1 =6 số có ba chữ số chia hết cho 3
Mỗi bộ gồm ba chữ số rất khác nhau và có một chữ số 0 nên ta viết được 2*2*1 = 4 số có ba chữ số chia hết cho 3
Vậy theo quy tắc cộng ta có: 6*4 +4*3 =36 số có 3 chữ số chia hết cho 3
Chọn đáp án là A
Nhận xét :
– Học sinh hoàn toàn có thể nhầm vận dụng quy tắc nhân cho kết quả: 64 *43 = 82944 số (phương án C)
– Học sinh hoàn toàn có thể không để ý điều kiên a≠0 nên cho kết quả 6*7 =42 (phương án B)
– Học sinh hoàn toàn có thể liệt kê bộ ba chữ số thoả mãn (*) không đủ nên không thể cho những kết quả A,B,C (phương án D)
 Exam24h Support
Exam24h Support
Gửi 3 năm trước đó
1045 đâu – Đỗ Trị –Thêm phản hồi
Câu vấn đáp của bạn

Câu hỏi liên quan
Reply
1
0
Chia sẻ
Chia Sẻ Link Tải Từ 0 1 2 3 4, 5 lập được bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 5 miễn phí
Bạn vừa đọc nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Video Từ 0 1 2 3 4, 5 lập được bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 5 tiên tiến và phát triển nhất và Chia Sẻ Link Cập nhật Từ 0 1 2 3 4, 5 lập được bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 5 miễn phí.

Hỏi đáp vướng mắc về Từ 0 1 2 3 4, 5 lập được bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 5
Nếu sau khi đọc nội dung bài viết Từ 0 1 2 3 4, 5 lập được bao nhiêu số có 3 chữ số rất khác nhau chia hết cho 5 vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Ad lý giải và hướng dẫn lại nha
#Từ #lập #được #bao #nhiêu #số #có #chữ #số #khác #nhau #chia #hết #cho