Mẹo Hướng dẫn Cách về mặt phẳng tuy nhiên tuy nhiên với đường thẳng 2022
Bạn đang tìm kiếm từ khóa Cách về mặt phẳng tuy nhiên tuy nhiên với đường thẳng được Cập Nhật vào lúc : 2022-02-01 08:56:03 . Với phương châm chia sẻ Thủ Thuật về trong nội dung bài viết một cách Chi Tiết Mới Nhất. Nếu sau khi tìm hiểu thêm Post vẫn ko hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha.
Hai mặt phẳng tuy nhiên tuy nhiên là gì? Cần Đk nào để hai mặt phẳng hoàn toàn có thể tuy nhiên tuy nhiên với nhau? Hai mặt phẳng tuy nhiên tuy nhiên có những tính chất gì? Cách chứng tỏ 2 mặt phẳng tuy nhiên tuy nhiên? Các dạng bài tập về 2 mặt phẳng tuy nhiên tuy nhiên? Tất cả những vướng mắc này sẽ tiến hành giải đáp dưới đây. Hãy cùng DINHNGHIA.VN tìm làm rõ ràng qua nội dung bài viết sau nhé!.
Nội dung chính
- Tìm hiểu 2 mặt phẳng tuy nhiên tuy nhiên
- Định nghĩa hai mặt phẳng tuy nhiên tuy nhiên
- Định lý về 2 mặt phẳng tuy nhiên tuy nhiên
- Tính chất của hai mặt phẳng tuy nhiên tuy nhiên
- Các dạng bài tập hai mặt phẳng tuy nhiên tuy nhiên
- Dạng 1: Chứng minh hai mặt phẳng tuy nhiên tuy nhiên
- Dạng 2: Xác định thiêt diện của (α) với hình chóp lúc biết (α)// (β) cho trước.
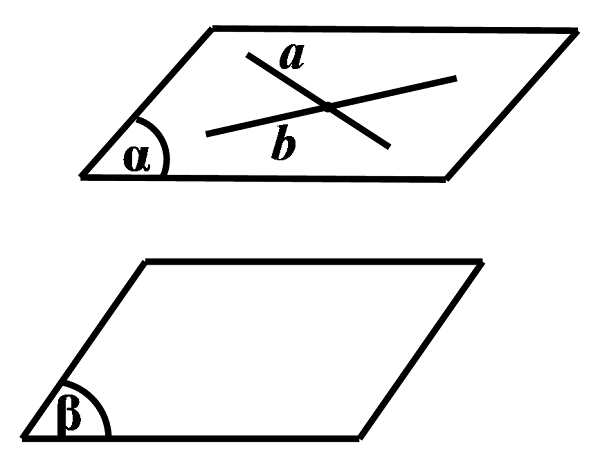
- Nếu mặt phẳng (α) chứa hai tuyến phố thẳng cắt nhau a, b và a, b cùng tuy nhiên tuy nhiên với mặt phẳng (β ) thì (α ) // (β ) => này cũng là yếu tố kiện để 2 mặt phẳng (α) và (β) tuy nhiên tuy nhiên với nhau.
- Cho 2 mặt phẳng tuy nhiên tuy nhiên. Nếu một mặt phẳng cắt mặt phẳng này thì cũng cắt mặt phẳng kia và hai giao tuyến tuy nhiên tuy nhiên với nhau.
- Ba mặt phẳng đôi một tuy nhiên tuy nhiên chắn trên hai cát tuyến bất kì những đoạn thẳng tương ứng tỉ lệ. (định lý này còn được nghe biết với tên thường gọi: định lý Ta lét trong không khí).
- Nếu a // (Q.) thì qua a có một và chỉ một mặt phẳng tuy nhiên tuy nhiên với (Q.).
- Hai mặt phẳng phân biệt cùng tuy nhiên tuy nhiên với mặt phẳng thứ 3 thì tuy nhiên tuy nhiên với nhau.
- Cách 1: Chứng minh trong mặt phẳng này còn có hai tuyến phố thẳng cắt nhau và tuy nhiên tuy nhiên với mặt phẳng kia.
- Tổng quát: a thuộc (α), b thuộc (α), a và b giao nhau tại I.
- Ta cần chứng tỏ: a // (β) và b // (β). Suy ra: (α) // (β)
- Cách 2: chứng tỏ hai mặt phẳng đó cùng tuy nhiên tuy nhiên với mặt phẳng thứ 3
- (α) // (Ɣ) và (β)// (Ɣ) => (α) // (β).
Tìm hiểu 2 mặt phẳng tuy nhiên tuy nhiên
Định nghĩa hai mặt phẳng tuy nhiên tuy nhiên
Theo định nghĩa thì hai mặt phẳng (α) và (β) được gọi là tuy nhiên tuy nhiên nếu chúng không còn điểm chung. Khi đó ta kí hiệu: (α) // (β) hay (β) // (α).
Định lý về 2 mặt phẳng tuy nhiên tuy nhiên
Đối với chuyên đề 2 mặt phẳng tuy nhiên tuy nhiên, ta có một số trong những định lý quan trọng cần ghi nhớ:
Hệ quả: Nếu mặt phẳng (α) chứa hai tuyến phố thẳng cắt nhau a, b và a, b lần lượt tuy nhiên tuy nhiên với hai tuyến phố thẳng a, b nằm trong mặt phẳng (β) thì mặt phẳng ( α) tuy nhiên tuy nhiên với mặt phẳng (β ).
Tính chất của hai mặt phẳng tuy nhiên tuy nhiên
*Tính chất 1: Qua một điểm nằm ngoài 1 mặt phẳng, có một và chỉ một mặt phẳng tuy nhiên tuy nhiên với mặt phẳng đó.
Cách dựng: Trong mặt phẳng (P), dựng 2 đường thẳng a,b cắt nhau. Qua giao điểm O, ta dụng a1//a và b1//b.
Vậy mặt phẳng chứa 2 đường thẳng a1,b1 sẽ tuy nhiên tuy nhiên với (P).
Từ đó ta có những hệ quả:
*Tính chất 2: Nếu (P)//(Q.) thì mặt phẳng (R) cắt (P) thì sẽ cắt (Q.) và những giao tuyến của chúng tuy nhiên tuy nhiên với nhau.
Các dạng bài tập hai mặt phẳng tuy nhiên tuy nhiên
Hai mặt phẳng tuy nhiên tuy nhiên lớp 12 cũng luôn có thể có đề cập tới. Vậy có những dạng bài tập nào về phần này? Hãy cùng tìm hiểu một số trong những dạng bài tập 2 mặt phẳng tuy nhiên tuy nhiên có lời giải dưới đây.
Dạng 1: Chứng minh hai mặt phẳng tuy nhiên tuy nhiên
Có 2 cách làm với dạng bài tập này:
Dạng 2: Xác định thiêt diện của (α) với hình chóp lúc biết (α)// (β) cho trước.
Cách giải: ta cần vận dụng những tính chất sau: khi (α) // (β) thì (α) sẽ tuy nhiên tuy nhiên với toàn bộ những đường thẳng có trong (β). Lúc này, ta chuyển về dạng thiết diện tuy nhiên tuy nhiên với đường thẳng.
Ta có: (α) // (β) và (Ɣ) giao (β) tại d. Suy ra: (α) sẽ giao với (Ɣ) tại d//d.
Đường thẳng d nằm trong (β) nên ta sé xét những mặt phẳng có trong hình chóp và chứa d. Khi đó, (α) // d nên sẽ cắt những mặt phẳng chứa d theo những giao tuyến tuy nhiên tuy nhiên với d.
Bên cạnh 2 dạng bài tập trên, những bạn cần lưu ý dạng bài tập trắc nghiệm về 2 mặt phẳng tuy nhiên tuy nhiên oxyz. Đây là một dạng không thể bỏ qua trong chuyên đề 2 mặt phẳng tuy nhiên tuy nhiên 12. Để hiểu hơn về phần kiến thức và kỹ năng này, bạn cũng hoàn toàn có thể tìm kiếm 2 mặt phẳng tuy nhiên tuy nhiên violet để tìm hiểu thêm những bài soạn trực tuyến.
Có thể thấy, hai mặt phẳng tuy nhiên tuy nhiên là một chuyên đề rất khó, nhưng chỉ việc bạn ghi nhớ những định lý và tính chất của hai mặt phẳng tuy nhiên tuy nhiên thì việc học sẽ đơn thuần và giản dị hơn thật nhiều. Đừng quên truy vấn DINHNGHIA.VN để mày mò nhiều kiến thức và kỹ năng hay và có ích hơn thế nữa nhé!.
Xem rõ ràng qua bài giảng dưới đây nhé:
(Nguồn: www.youtube.com)
Xem thêm >>> Đường thẳng vuông góc với mặt phẳng: Lý thuyết và Các dạng bài tập
Xem thêm >>> Hai mặt phẳng vuông góc là gì? Bài tập 2 mặt phẳng vuông góc
Rate this post
Reply
0
0
Chia sẻ
Chia Sẻ Link Cập nhật Cách về mặt phẳng tuy nhiên tuy nhiên với đường thẳng miễn phí
Bạn vừa tìm hiểu thêm nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Video Cách về mặt phẳng tuy nhiên tuy nhiên với đường thẳng tiên tiến và phát triển nhất và Share Link Cập nhật Cách về mặt phẳng tuy nhiên tuy nhiên với đường thẳng Free.

Giải đáp vướng mắc về Cách về mặt phẳng tuy nhiên tuy nhiên với đường thẳng
Nếu sau khi đọc nội dung bài viết Cách về mặt phẳng tuy nhiên tuy nhiên với đường thẳng vẫn chưa hiểu thì hoàn toàn có thể lại Comment ở cuối bài để Mình lý giải và hướng dẫn lại nha
#Cách #về #mặt #phẳng #tuy nhiên #tuy nhiên #với #đường #thẳng