Cách tính diện tích bề mặt hình trụ -Thủ Thuật Mới

Mẹo Hướng dẫn Cách tính diện tích s quy hoạnh mặt phẳng hình trụ 2022

Pro đang tìm kiếm từ khóa Cách tính diện tích s quy hoạnh mặt phẳng hình trụ được Update vào lúc : 2022-12-13 15:47:07 . Với phương châm chia sẻ Mẹo về trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc Post vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.

Trong toán học (nhất là hình học ) và khoa học, bạn thường sẽ cần tính diện tích s quy hoạnh mặt phẳng, thể tích hoặc chu vi của nhiều hình dạng. Cho dù đó là hình cầu hay hình tròn trụ, hình chữ nhật hay hình lập phương , hình chóp hay hình tam giác, mỗi hình dạng đều phải có những công thức rõ ràng mà bạn phải tuân theo để đã có được số đo đúng chuẩn.

Nội dung chính

• Diện tích mặt phẳng và thể tích của một hình cầu


• Diện tích mặt phẳng và khối lượng của hình nón


• Diện tích mặt phẳng và thể tích của xi lanh


• Diện tích mặt phẳng và thể tích của lăng kính hình chữ nhật


• Diện tích mặt phẳng và thể tích của một kim tự tháp


• Diện tích mặt phẳng và thể tích của lăng kính


• Diện tích của một khu vực vòng tròn


• Diện tích hình elip


• Diện tích và chu vi của một tam giác


• Diện tích và chu vi của một hình tròn trụ


• Diện tích và chu vi của một hình bình hành


• Diện tích và chu vi của hình chữ nhật


• Diện tích và chu vi hình vuông vắn


• Diện tích và chu vi của hình thang


• Diện tích và chu vi của một hình lục giác


• Diện tích và chu vi của một hình bát giác


• 
  

Chúng ta sẽ kiểm tra những công thức bạn sẽ cần để tìm ra diện tích s quy hoạnh mặt phẳng và thể tích của những hình ba chiều cũng như diện tích s quy hoạnh và chu vi của những hình hai chiều . Bạn hoàn toàn có thể nghiên cứu và phân tích bài học kinh nghiệm tay nghề này để tìm hiểu từng công thức, tiếp theo đó lưu lại để tìm hiểu thêm nhanh cho lần sau khi cần. Tin tốt là mỗi công thức sử dụng nhiều phép đo cơ bản giống nhau, vì vậy việc học mỗi công thức mới sẽ thuận tiện và đơn thuần và giản dị hơn một chút ít.




01trên 16




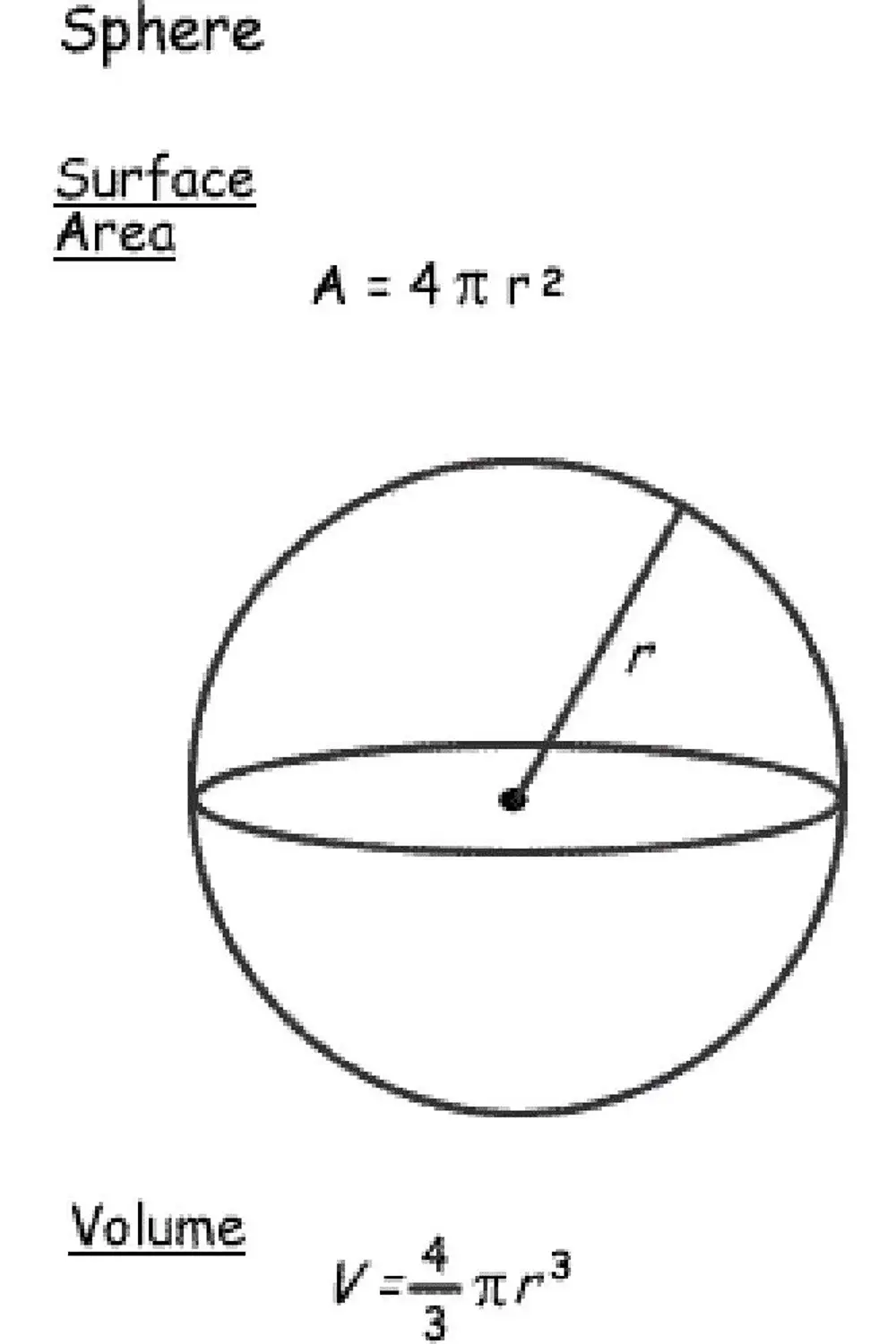
Diện tích mặt phẳng và thể tích của một hình cầu




D. Russell




Hình tròn ba chiều được gọi là hình cầu. Để tính diện tích s quy hoạnh mặt phẳng hoặc thể tích của một hình cầu, bạn nên phải ghi nhận bán kính ( r ). Bán kính là khoảng chừng cách từ tâm của hình cầu đến cạnh và nó luôn bằng nhau, bất kể bạn đo từ điểm nào trên cạnh của hình cầu.




Khi bạn có bán kính, những công thức khá đơn thuần và giản dị để nhớ. Cũng như với chu vi của vòng tròn , bạn sẽ nên phải sử dụng pi ( π ). Nói chung, bạn hoàn toàn có thể làm tròn số vô hạn này thành 3,14 hoặc 3,14159 (phân số được đồng ý là 22/7).



• Diện tích mặt phẳng = 4πr 2


• Khối lượng = 4/3 πr 3



02trên 16




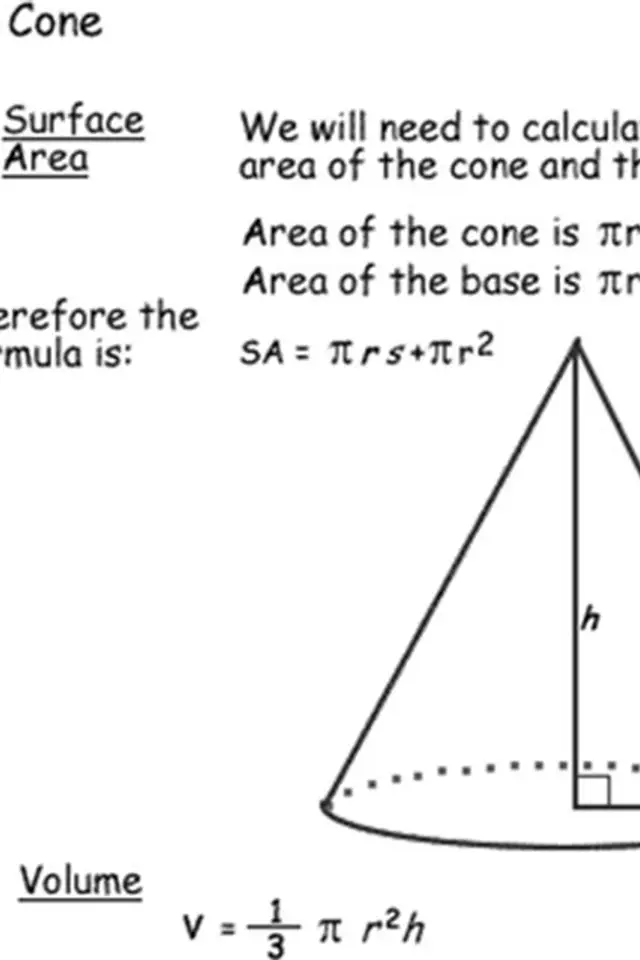
Diện tích mặt phẳng và khối lượng của hình nón




D. Russell




Hình nón là một hình chóp có đáy là hình tròn trụ có những mặt dốc gặp nhau tại một điểm ở chính giữa. Để tính diện tích s quy hoạnh mặt phẳng hoặc thể tích của nó, bạn phải ghi nhận bán kính của cơ sở và chiều dài của mặt bên.




Nếu bạn chưa chắc như đinh, bạn hoàn toàn có thể tìm ( những ) độ dài cạnh bằng phương pháp sử dụng bán kính ( r ) và độ cao của hình nón ( h ).



• s = (r2 + h2)



Với điều này, bạn hoàn toàn có thể tìm thấy tổng diện tích s quy hoạnh mặt phẳng, là tổng diện tích s quy hoạnh của phần đáy và diện tích s quy hoạnh của mặt bên.



• Diện tích cơ sở: πr 2


• Diện tích của mặt: πrs


• Tổng diện tích s quy hoạnh mặt phẳng = πr 2 + πrs



Để tìm thể tích của một hình cầu, bạn chỉ việc bán kính và độ cao.



• Khối lượng = 1/3 πr 2 giờ



03trên 16




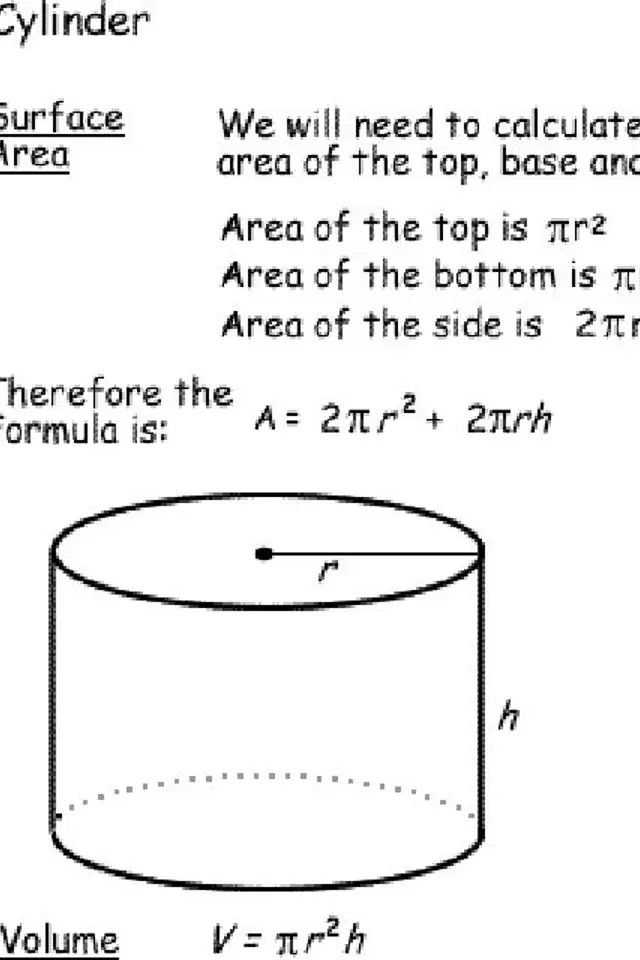
Diện tích mặt phẳng và thể tích của xi lanh




D. Russell




Bạn sẽ thấy rằng một hình trụ dễ thao tác hơn nhiều so với một hình nón. Hình dạng này còn có đáy là hình tròn trụ và những cạnh thẳng tuy nhiên tuy nhiên. Điều này nghĩa là để tìm diện tích s quy hoạnh hoặc thể tích mặt phẳng của nó, bạn chỉ việc bán kính ( r ) và độ cao ( h ).




Tuy nhiên, bạn cũng phải tính đến việc có cả đỉnh và đáy, đó là nguyên do tại sao bán kính phải được nhân với hai cho diện tích s quy hoạnh mặt phẳng.



• Diện tích mặt phẳng = 2πr 2 + 2πrh


• Khối lượng = πr 2 giờ



04trên 16




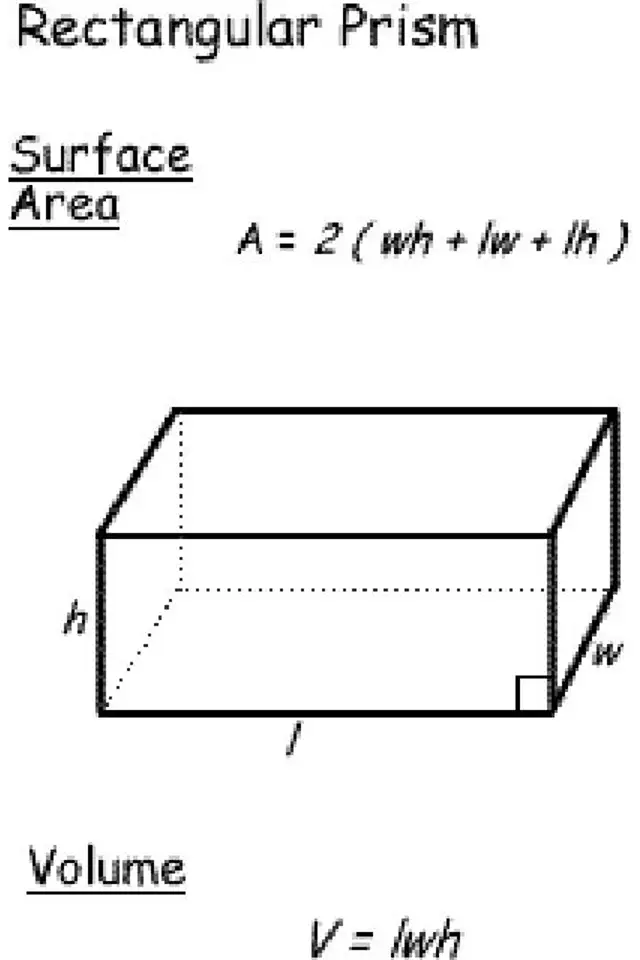
Diện tích mặt phẳng và thể tích của lăng kính hình chữ nhật




D. Russell




Một hình chữ nhật có ba kích thước trở thành hình lăng trụ (hoặc hình hộp) hình hộp chữ nhật. Khi toàn bộ những cạnh có kích thước bằng nhau, nó sẽ trở thành một khối lập phương. Dù bằng phương pháp nào, việc tìm diện tích s quy hoạnh mặt phẳng và thể tích cũng yêu cầu những công thức giống nhau.




Đối với những điều này, bạn sẽ nên phải ghi nhận chiều dài ( l ), độ cao ( h ) và chiều rộng ( w ). Với một khối lập phương, cả ba sẽ giống nhau.



• Diện tích mặt phẳng = 2 (lh) + 2 (lw) + 2 (wh)


• Âm lượng = lhw



05trên 16




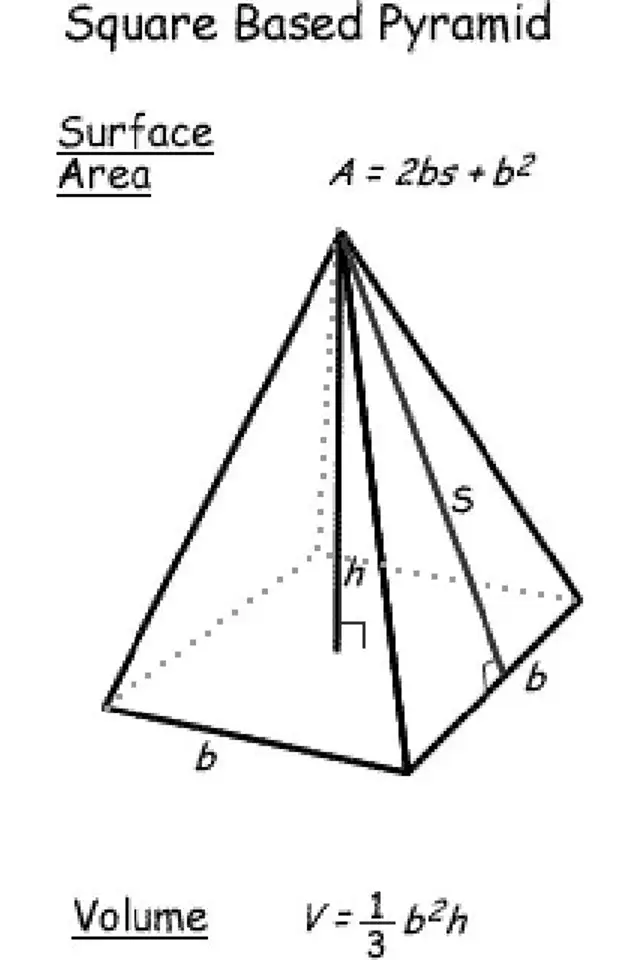
Diện tích mặt phẳng và thể tích của một kim tự tháp




D. Russell




Một hình chóp có đáy là hình vuông vắn và những mặt được tạo bởi những tam giác đều tương đối dễ thao tác.




Bạn sẽ nên phải ghi nhận số đo cho một chiều dài của cơ sở ( b ). Chiều cao ( h ) là khoảng chừng cách từ mặt đáy đến tâm của hình chóp. Phía ( s ) là chiều dài của một khuôn mặt của kim tự tháp, từ cơ sở tới điểm trên cao nhất.



• Diện tích mặt phẳng = 2bs + b 2


• Khối lượng = 1/3 b 2 h



Một cách khác để tính điều này là sử dụng chu vi ( P ) và diện tích s quy hoạnh ( A ) của hình cơ sở. Điều này hoàn toàn có thể được sử dụng trên một kim tự tháp có hình chữ nhật hơn là hình vuông vắn.



• Diện tích mặt phẳng = (½ x P xs) + A


• Khối lượng = 1/3 Ah



06trên 16




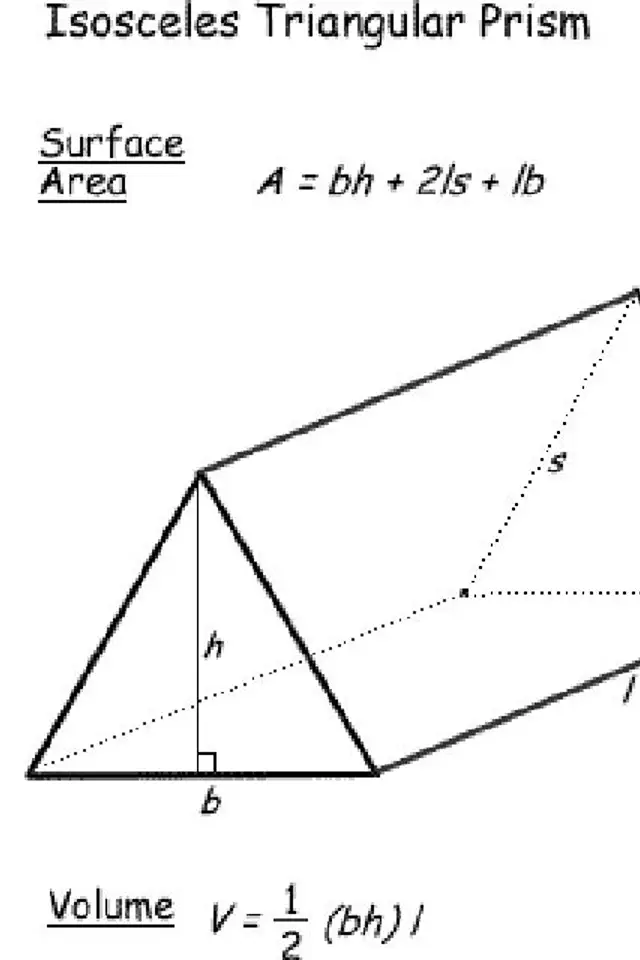
Diện tích mặt phẳng và thể tích của lăng kính




D. Russell




Khi chuyển từ hình chóp sang hình lăng trụ tam giác cân, bạn cũng phải tính đến chiều dài ( l ) của hình đó. Hãy nhớ những chữ viết tắt của cơ sở ( b ), độ cao ( h ) và ( những ) cạnh vì chúng thiết yếu cho những phép tính này.



• Diện tích mặt phẳng = bh + 2ls + lb


• Khối lượng = 1/2 (bh) l



Tuy nhiên, một lăng kính hoàn toàn có thể là bất kỳ chồng hình dạng nào. Nếu phải xác lập diện tích s quy hoạnh hoặc thể tích của một hình lăng trụ lẻ, ta hoàn toàn có thể nhờ vào diện tích s quy hoạnh ( A ) và chu vi ( P ) của hình đáy. Nhiều lần, công thức này sẽ sử dụng độ cao của lăng kính, hoặc chiều sâu ( d ), thay vì chiều dài ( l ), tuy nhiên bạn hoàn toàn có thể thấy một trong hai chữ viết tắt.



• Diện tích mặt phẳng = 2A + Pd


• Khối lượng = Quảng cáo



07trên 16




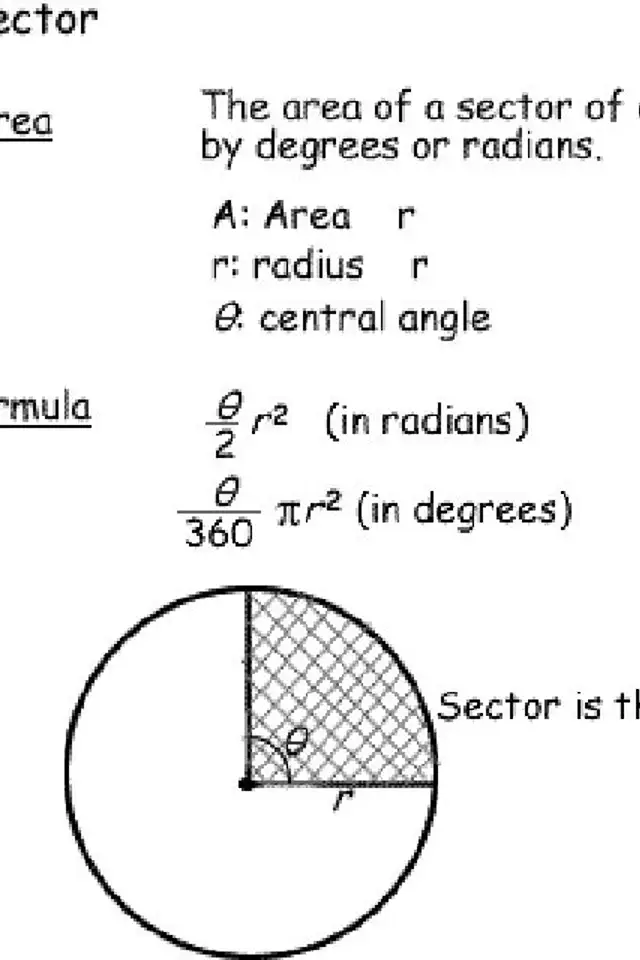
Diện tích của một khu vực vòng tròn




D. Russell




Diện tích của một cung của hình tròn trụ hoàn toàn có thể được xem bằng độ (hoặc radian thường được sử dụng trong giải tích). Đối với điều này, bạn sẽ cần bán kính ( r ), pi ( π ) và góc TT ( θ ).



• Diện tích = θ / 2 r 2 (tính bằng radian)


• Diện tích = θ / 360 πr 2 (tính bằng độ)



08trên 16




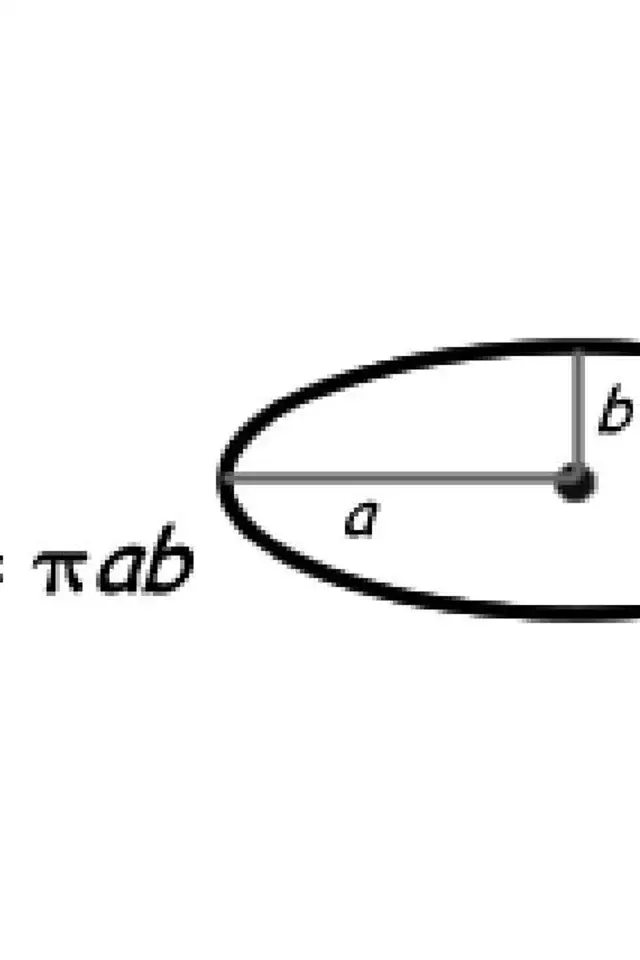
Diện tích hình elip




D. Russell




Hình elip còn được gọi là hình bầu dục và về cơ bản, nó là một hình tròn trụ thuôn dài. Khoảng cách từ tâm điểm đến mặt bên không đổi, điều này làm cho công thức tìm diện tích s quy hoạnh của nó hơi phức tạp.




Để sử dụng công thức này, bạn phải ghi nhận:



• Semiminor Axis ( a ): Khoảng cách ngắn nhất giữa tâm điểm và cạnh.


• Semimajor Axis ( b ): Khoảng cách xa nhất giữa tâm điểm và cạnh.



Tổng của hai điểm này sẽ không còn đổi. Đó là nguyên do tại sao toàn bộ chúng ta hoàn toàn có thể sử dụng công thức sau để tính diện tích s quy hoạnh của bất kỳ hình elip nào.



• Diện tích = πab



Đôi khi, bạn hoàn toàn có thể thấy công thức này được viết với r 1 (bán kính 1 hoặc trục bán kính) và r 2 (bán kính 2 hoặc trục bán nguyệt) thay vì a và b .



• Diện tích = πr 1 r 2



09trên 16




Diện tích và chu vi của một tam giác




Hình tam giác là một trong những hình đơn thuần và giản dị nhất và việc tính chu vi của hình ba cạnh này khá thuận tiện và đơn thuần và giản dị. Bạn sẽ nên phải ghi nhận độ dài của toàn bộ ba cạnh ( a, b, c ) để đo toàn bộ chu vi.



• Chu vi = a + b + c



Để tìm ra diện tích s quy hoạnh của tam giác, bạn sẽ chỉ việc độ dài của đáy ( b ) và độ cao ( h ), được đo từ đáy đến đỉnh của tam giác. Công thức này vận dụng cho bất kỳ tam giác nào, bất kể những cạnh có bằng nhau hay là không.



• Diện tích = 1/2 bh



10trên 16




Diện tích và chu vi của một hình tròn trụ




Tương tự như một hình cầu, bạn sẽ nên phải ghi nhận bán kính ( r ) của một hình tròn trụ để tìm đường kính ( d ) và chu vi ( c ) của nó. Hãy nhớ rằng một đường tròn là một hình elip có tầm khoảng chừng cách từ tâm đến mọi cạnh (bán kính) bằng nhau, vì vậy bạn đo ở vị trí nào trên cạnh không quan trọng.



• Đường kính (d) = 2r


• Chu vi (c) = πd hoặc 2πr



Hai số đo này được sử dụng trong một công thức để tính diện tích s quy hoạnh hình tròn trụ. Điều quan trọng cần nhớ là tỷ số giữa chu vi hình tròn trụ và đường kính của nó bằng pi ( π ).



• Diện tích = πr 2



11trên 16




Diện tích và chu vi của một hình bình hành




Hình bình hành có hai tập hợp những cạnh trái chiều tuy nhiên tuy nhiên với nhau. Hình là một tứ giác nên nó có bốn cạnh: hai cạnh có độ dài ( a ) và hai cạnh có độ dài khác ( b ).




Để tìm ra chu vi của bất kỳ hình bình hành nào, hãy sử dụng công thức đơn thuần và giản dị sau:



• Chu vi = 2a + 2b



Khi bạn cần tìm diện tích s quy hoạnh hình bình hành, bạn sẽ cần độ cao ( h ). Đây là khoảng chừng cách giữa hai cạnh tuy nhiên tuy nhiên. Cơ sở ( b ) cũng khá được yêu cầu và đấy là chiều dài của một trong những cạnh.



• Diện tích = bxh



Hãy nhớ rằng b trong công thức diện tích s quy hoạnh rất khác với b trong công thức chu vi. Bạn hoàn toàn có thể sử dụng bất kỳ cạnh nào được ghép nối thành a và b khi tính chu vi tuy nhiên thông thường toàn bộ chúng ta sử dụng cạnh vuông góc với độ cao.




12trên 16




Diện tích và chu vi của hình chữ nhật




Hình chữ nhật cũng là một hình tứ giác. Không in như hình bình hành, những góc bên trong luôn bằng 90 độ. Ngoài ra, những cạnh trái chiều nhau sẽ luôn đo cùng độ dài.




Để sử dụng những công thức về chu vi và diện tích s quy hoạnh, bạn sẽ cần đo chiều dài ( l ) và chiều rộng ( w ) của hình chữ nhật .



• Chu vi = 2h + 2w


• Diện tích = hxw



13trên 16




Diện tích và chu vi hình vuông vắn




Hình vuông còn dễ hơn hình chữ nhật vì nó là hình chữ nhật có bốn cạnh bằng nhau. Điều đó nghĩa là bạn chỉ việc biết chiều dài của ( những ) cạnh để tìm chu vi và diện tích s quy hoạnh của nó.



• Chu vi = 4 giây


• Diện tích = s 2



14trên 16




Diện tích và chu vi của hình thang




Hình thang là một hình tứ giác hoàn toàn có thể trông in như một thử thách, nhưng nó thực sự khá thuận tiện và đơn thuần và giản dị. Đối với hình dạng này, chỉ có hai cạnh tuy nhiên tuy nhiên với nhau, tuy nhiên cả bốn cạnh hoàn toàn có thể có độ dài rất khác nhau. Điều này nghĩa là bạn sẽ nên phải ghi nhận độ dài của mỗi cạnh ( a, b 1 , b 2 , c ) để tìm chu vi của hình thang.



• Chu vi = a + b 1 + b 2 + c



Để tìm diện tích s quy hoạnh của một hình thang, bạn cũng tiếp tục cần độ cao ( h ). Đây là khoảng chừng cách giữa hai cạnh tuy nhiên tuy nhiên.



• Diện tích = 1/2 (b 1 + b 2 ) xh



15trên 16




Diện tích và chu vi của một hình lục giác




Một đa giác sáu cạnh có những cạnh bằng nhau là một hình lục giác đều. Độ dài mỗi cạnh bằng bán kính ( r ). Mặc dù nó có vẻ như thể một hình dạng phức tạp, nhưng tính chu vi là một yếu tố đơn thuần và giản dị khi nhân bán kính với sáu cạnh.



• Chu vi = 6r



Tính ra diện tích s quy hoạnh của một hình lục giác khó hơn một chút ít và bạn sẽ phải ghi nhớ công thức này:



• Diện tích = (33 / 2) r 2



16trên 16




Diện tích và chu vi của một hình bát giác




Một hình bát giác đều tương tự như một hình lục giác, tuy nhiên đa giác này còn có tám cạnh bằng nhau. Để tìm chu vi và diện tích s quy hoạnh của hình này, bạn sẽ cần chiều dài của một cạnh ( a ).



• Chu vi = 8a


• Diện tích = (2 + 22) a 2



Reply

6

0

Chia sẻ




Chia Sẻ Link Download Cách tính diện tích s quy hoạnh mặt phẳng hình trụ miễn phí




Bạn vừa Read nội dung bài viết Với Một số hướng dẫn một cách rõ ràng hơn về Clip Cách tính diện tích s quy hoạnh mặt phẳng hình trụ tiên tiến và phát triển nhất và Share Link Down Cách tính diện tích s quy hoạnh mặt phẳng hình trụ Free.





Thảo Luận vướng mắc về Cách tính diện tích s quy hoạnh mặt phẳng hình trụ




Nếu sau khi đọc nội dung bài viết Cách tính diện tích s quy hoạnh mặt phẳng hình trụ vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Admin lý giải và hướng dẫn lại nha

#Cách #tính #diện #tích #bề #mặt #hình #trụ