Mẹo Hướng dẫn Có mấy cách xác lập tập hợp 2022
Bạn đang tìm kiếm từ khóa Có mấy cách xác lập tập hợp được Update vào lúc : 2022-11-29 13:47:04 . Với phương châm chia sẻ Kinh Nghiệm Hướng dẫn trong nội dung bài viết một cách Chi Tiết 2022. Nếu sau khi đọc nội dung bài viết vẫn ko hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha.
Vậy làm thế nào để xác lập một tập hợp? tập hợp rỗng (trống) là tập ra làm sao? trên tập hợp có những phép toán gì? và tập hợp có những dạng toán nào? toàn bộ chúng ta cùng tìm câu vấn đáp qua nội dung bài viết khối mạng lưới hệ thống lại kiến thức và kỹ năng về tập hợp và cách giải những dạng toán về tập hợp dưới đây.
I. Lý thuyết về Tập hợp
1. Tập hợp
– Cho tập hợp A
+ Nếu a là thành phần thuộc tập A ta viết a A.
+ Nếu a là thành phần không thuộc tập a ta viết a A.
2.Một tập hợp xác lập bởi
a) Viết tập hợp bằng phương pháp liệt kê những thành phần của tập hợp
– Viết toàn bộ những thành phần của tập hợp vào giữa dấu, những thành phần cách nhau bằng dấu phẩy (,) hoặc chấm phẩy (;).
Ví dụ: A = 1,2,3,4,5,6
b) Viết tập hợp bằng phương pháp nếu tính chất đặc trưng của tập
– Chỉ ra tính chất đặc trưng cho những thành phần của tập đó
Ví dụ:ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/15549777762qtwl97gxg_1600692648.gif"/>
– Ta thường minh hoạ tập hợp bằng một đường cong khép kín gọi là biểu đồ ven.
Biểu diễn tập hợp bằng biểu đồ VEN
3. Tập hợp rỗng
– Là tập hợp không chứa thành phần nào, Ký hiệu làØ
A Øx: x A
4. Tập hợp con của một tập hợp
– Cho 2 tập A, B: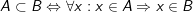 
– Lưu ý:
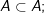
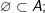
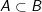và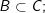
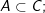
Tập A có n thành phần thì A có 2n tập con.
5. Hai tập hợp bằng nhau
– Cho 2 tập A, B: A = B A B vàBA
6. Một số tập hợp số
a) Các tập hợp số
– Tập hợp số tự nhiên:ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/15549777876gr5upv94r_1600692650.gif"/>
– Tập hợp số tự nhiên khác 0: ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/15549777894njwlam8kr_1600692650.gif"/>
– Tập hợp số nguyên:ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/15549777914s1jayzym0_1600692650.gif"/>
– Tâp hợp số hữu tỉ:eq 0
ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/1554977793cp7k4mx7af_1600692651.gif"/>
Tập hợp những số hữu tỉ gồm những số thập phân hữu hạn và thập phân vô hạn tuần hoàn
– Tập hợp số vô tỉ: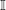
= tập hợp những số thập phân vô hạn không tuần hoàn
– Tập hợp số thực: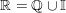
gồm tập hợp toàn bộ những số hữu tỉ và vô tỉ được màn biểu diễn bằng trục số.
b) Mối quan hệ Một trong những tập hợp số
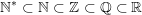
biểu đồ VEN thể hiện quan hệ Một trong những tập số
7. Các phép toán trên tập hợp
a) Phép giao
ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/1554977799qhqchov801_1600692652.gif"/>
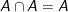
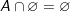
b) Phép hội
ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/1554977804qqbur4csiz_1600692653.gif"/>
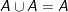
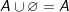
c) Phép hiệu
AB = x
AA =
A = A
ABBA
d) Phép lấy phần bù: Khi B A: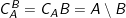
II. Các dạng bài tập toán về Tập hợp
Dạng 1. Xác định tập hợp
* Phương pháp:
– Liệt kê những thành phần của tập hợp: A = a1, a2, a3,…
– Nêu tính đặc trưng của tập hợp: A = p.(x)
Ví dụ 1: Tìm tập hợp những số tự nhiên chẵn khác 0 và nhỏ hơn 10
* Hướng dẫn:
– Ta liệt kê những thành phần: A = 2,4,6,8 hoặc A = x = BS(2) và x < 10
Ví dụ 2: Tìm tập hợp những nghiệm của phương trình: x(x-1)(x-2)(x2-1) = 0
* Hướng dẫn:
– Liệt kê: A = 0, -1, 1, 2
– A =x Z A = x Z
Ví dụ 3: Viết tập hợp A = 2,3 bằng phương pháp nêu ra tính chất đặc trưng của nó.
* Hướng dẫn:
– Ta hoàn toàn có thể viết như sau:
A = 1 < x < 4
A = 2 x3
A = (x-2)(x-3) = 0
A =xN
Dạng 2.Tập hợp con, Tập hợp bằng nhau
* Phương pháp:Áp dụng định nghĩa
+)
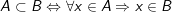
+) A Bx A x B
+) A = B A B và B A
+) A B A BhoặcB A
Ví dụ 1: Cho 2 tập hợp A = x3 – 2×2 – x + 2 = 0 và B = x2- 3x + 2 = 0 hãy đặt dấu và giữa A và B.
* Hướng dẫn:
– Ta liệt kê những thành phần tập A và B: A = -1; 1; 2 , B = 1; 2
B A
Ví dụ 2: Cho A = x Tìm những tập con của A và tập con đó có chứa thành phần 0.
* Hướng dẫn:
– Liệt kê số thành phần của A = 0; 1; 2vậy tập A có 23 = 8 tập con như sau:
0, 1, 2, 0;1, 0;2, 1;2 , 0;1;2 vàØ
Các tập có chứa thành phần 0 là:0, 0;1, 0;2, 0;1;2
Ví dụ 3: Chotập hợp,
ight " src="https://hayhochoi.vn/uploads/news/wyswyg/2020_09/1555072177tbwvl8oi52_1600692654.gif"/>
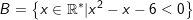
Xác định =, giữa A và B
* Hướng dẫn:
– Ta có:A = [-2;0) U (0;3] và B = (-2;0) U (0;3)
A B
Ví dụ 4: Cho những tập hợp: E = -3; 4, F = -3; x2 , G = -3; x2; y. Xác định x, y để E=F=G.
* Hướng dẫn:
– ĐểE = F thì x2 = 4 x = 2 hoặc x = -2
– Để F = G thì y = – 3 hoặc y = x2 = 4
Để E = F = G thì x =±2 và y = -3 hoặc y = 4;
Dạng 3. Các phép toán trên tập hợp, Giao, Hợp, Hiệu
* Phương pháp:Áp dụng định nghĩa
– Liệt kê A, B
– A B : Lấy những thành phần giống nhau của A và B
– A U B : Lấy toàn bộ những thành phần của A, của B và củaA B (chung)
– A B: Lấy những thành phần của A và không phải của B
Ví dụ 1: Cho 2 tập hợp A = x2 – 4x + 3 0 và A = x2 – 3x +2 0 tính A U B,A B,A B vàBA.
* Hướng dẫn:
– Liệt kê: A = 1;3 và B = 1;2 ta có:
A U B = 1;2;3 ,A B = 1 ,A B = 3 ,BA = 2
Ví dụ 2:Cho 2 tập hợpA = x2- 4x + 3 = 0vàA = x2 -3x +2= 0tính A U B,A B,A B vàBA.
* Hướng dẫn:
-Liệt kê:A = [1;3] và B = [1;2] ta có:
A U B = [1;3] ,A B = [1;2] ,A B = (2;3] ,BA =
Dạng 4. Giải toán bằng biểu đồ VEN
* Phương pháp:Áp dụng định nghĩa
Ví dụ 1: Mỗi học viên của lớp 10A đều biết chơi cờ tướng hoặc cờ vua, biết rằng có 25em biết chơi cờ tướng, 30em biết chơi cờ vua, 15em biết chơi cả hai. Hỏi lớp 10A có bao nhiêu em chỉ biết chơi cờ tướng? Bao nhiêu em chỉ biết chơi cờ vua? Sĩ số lớp là bao nhiêu?
* Hướng dẫn:
– Ta vẽ biểu đồ VEN như sau:
– Dựa vào sơ đồ Ven ta suy ra số học viên chỉ biết chơi cờ tướng là 25 – 15 = 10.
– Số học viên chỉ biết chơi cờ vua là: 30 – 15 = 15.
– Do đó ta có sĩ số học viên của lớp 10A là: 10 + 15 + 15 = 40 học viên.
Ví dụ 2:Lớp 10B có 45học sinh, trong số đó có 25em thích môn Văn, 20 em thích môn Toán, 18em thích môn Sử, 66 em không thích môn nào, 55em thích cả ba môn. Hỏi số em thích chỉ một môn trong ba môn trên là bao nhiêu?
* Hướng dẫn:
– Ta vẽ biểu đồ VEN như sau:
– Gọi: a, b, ctheo thứ tự là số học viên chỉ thích môn Văn, Sử, Toán.
x là số học sịnh chỉ thích hai môn là Văn và Toán.
y là số học sịnh chỉ thích hai môn là Sử và Toán.
z là số học sịnh chỉ thích hai môn là Văn và Sử.
– Ta có số em thích tối thiểu một môn là 45 – 6 = 39.
– Dựa vào sơ đồ Ven ta có hệ phương trình:
(I)ight." src="https://cda.boxhoidap.com/cdnosa/co-may-cach-xac-dinh-tap-hop--b18c80655071d61908bba969f5642fe8.wepb"/>
– Giải hệ phương trình (I) bằng phương pháp cộng vế với vế 3 phương trình đầu ta có:
a + b + c + 2(x + y + z) + 15 = 63 kết phù thích hợp với phương trình cuối của hệ: x + y + z + a + b + c + 5 = 39 ta được:
a + b + c + 2(39 – 5 – a – b – c) + 15 = 63 a + b + c = 20
Vậy chỉ có 20 em thích chỉ một môn trong ba môn trên.
III. Một số bài tập về Tập hợp
Bài 1 trang 13 SGK Đại số 10:a) Cho A = x ϵ N .
Hãy liệt kê những thành phần của A.
b) Cho B = 2, 6, 12, 20, 30.
Hãy xách định B bằng phương pháp chỉ ra một tính chất đặc trưng cho những thành phần của nó.
c) Hãy liệt kê những thành phần của tập hợp những học viên lớp em cao trên 1m60.
* Lời giải bài 1 trang 13 SGK Đại số 10:
a) Tập hợp A là tập những số tự nhiên chia hết cho 3 và nhỏ hơn 20.
Vậy A = 0, 3, 6, 9, 12, 15, 18
b) Nhận thấy: 2 = 1.2 ; 6 = 2.3 ; 12 = 3.4 ; 20 = 4.5 ; 30 = 5.6
Vậy B = x = n(n + 1)
c) Ví dụ: C = Tuấn, Phúc, Trang, Linh.
Bài 2 trang 13 SGK Đại số 10:Trong hai tập hợp A, B dưới đây, tập hợp nào là tập hợp con của tập còn sót lại? Hai tập hợp A và B có bằng nhau không?
a) A là tập hợp những hình vuông vắn; B là tập hợp những hình thoi.
b) A = n N ; B = n N .
* Lời giải bài 2 trang 13 SGK Đại số 10:
a) Vì mỗi hình vuông vắn đều là một hình thoi nên A B. Có những hình thoi không phải là hình vuông vắn nên B A.
Vậy A B.
b) A = n N = 1; 2; 3; 6. B = n là một ước của 6 = 1; 2; 3; 6.
– Ta thấy A B và B A nên A = B.
Bài 3 trang 13 SGK Đại số 10:Tìm toàn bộ những tập con của tập hợp sau:
a) A = a; b
b) B = 0; 1; 2
* Lời giải bài 3 trang 13 SGK Đại số 10:
a) A = a; b có 22 = 4 những tập con đó là: ; a; b; a; b
b) B = 0; 1; 2 có 23 = 8 những tập con đó là: ; 0; 1 ; 2 ; 0, 1 ; 0, 2 ; 1, 2 ; 0; 1; 2.
Bài 3 trang 15 SGK Đại số 10:Trong số 45 học viên của lớp 10A có 15 bạn được xếp loại học lực giỏi, 20 bạn được xếp loại hạnh kiểm tốt, trong số đó có 10 bạn vừa học lực giỏi, vừa có hạnh kiểm tốt. Hỏi
a) Lớp 10A có bao nhiêu bạn được khen thưởng, biết rằng muốn được khen thưởng bạn đó phải học lực giỏi hoặc có hạnh kiểm tốt?
b) Lớp 10A có bao nhiêu bạn không được xếp loại học lực giỏi và chưa tồn tại hạnh kiểm tốt?
* Lời giải bài 3 trang 15 SGK Đại số 10:
a) Các bạn được HLG = 15.
– Các bạn được HKT = 20.
– Số bạn HLT + HKT = 10.
Số bạn được HKT mà không được HLG = 15 10 = 5.
Số bạn được HLG mà không được HKT = 20 10 = 10.
Vậy số bạn được khen thưởng = (số bạn được HKT mà không được HLG)
+ (số bạn được HLG mà không được HKT)
+ (số bạn vừa mới được HLG, vừa mới được HKT)
= 5 + 10 + 10 = 25 (bạn).
b) Số học viên không được xếp loại HLG và chưa tồn tại HKT là: 45 25 = 20 (bạn).
Reply
8
0
Chia sẻ
Chia Sẻ Link Tải Có mấy cách xác lập tập hợp miễn phí
Bạn vừa Read tài liệu Với Một số hướng dẫn một cách rõ ràng hơn về Review Có mấy cách xác lập tập hợp tiên tiến và phát triển nhất và Share Link Down Có mấy cách xác lập tập hợp Free.
Thảo Luận vướng mắc về Có mấy cách xác lập tập hợp
Nếu sau khi đọc nội dung bài viết Có mấy cách xác lập tập hợp vẫn chưa hiểu thì hoàn toàn có thể lại Comments ở cuối bài để Tác giả lý giải và hướng dẫn lại nha
#Có #mấy #cách #xác #định #tập #hợp