Câu 7 trang 121 SGK Hình học 11 Nâng cao
Đề bài
Một tứ diện được gọi là gần đều nếu các cạnh đối bằng nhau từng đôi một. Với tứ diện ABCD, chứng tỏ các tính chất sau là tương đương :
a. Tứ diện ABCD là gần đều ;
b. Các đoạn thẳng nối trung điểm cặp cạnh đối diện đôi một vuông góc với nhau ;
c. Các trọng tuyến (đoạn thẳng nối đỉnh với trọng tâm của mặt đối diện) bằng nhau ;
d. Tổng các góc tại mỗi đỉnh bằng 180˚
Lời giải chi tiết
* Chứng minh a b
Gọi M, N, P, Q, E, F lần lượt là trung điểm của AB, CD, BC, AD, AC, BD.
a b. Do AC = BD nên MNPQ là hình thoi, vì thế MN PQ. Tương tự ta có MN EF, PQ EF.
b) a. MPNQ là hình bình hành mà MN PQ nên MPNQ là hình thoi, tức là MP = MQ, từ đó AC = BD.
Tương tự như trên, ta cũng có BC = AD, AB = CD.
* Chứng minh a c
Gọi A, B lần lượt là trọng tâm của các tam giác BCD và ACD.
a) c. Ta có ΔBCD = ΔADC (c.c.c) nên BN = AN, từ đó AN = BN.
Vậy ΔAAN = ΔBBN (c.g.c), suy ra AA = BB.
Tương tự như trên, ta có điều phải chứng minh.
c) a. Do giả thiết ta có BB = AA, mà AA cắt BB tại G, AG = 3GA, BG = 3GB (xem BT 22, chương II, SGK), từ đó BG = AG và GA = GB. Các tam giác BGA và AGB bằng nhau nên BA = AB.
Như vậy BN = AN, mà :
\(\eqalign{ & A{C^2} + A{D^2} = 2A{N^2} + {{C{D^2}} \over 2} \cr & B{C^2} + B{D^2} = 2B{N^2} + {{C{D^2}} \over 2} \cr} \)
Do đó \(A{C^2} + A{D^2} = B{C^2} + B{D^2}\) (1)
Tương tự như trên ta có : \(C{A^2} + C{B^2} = D{A^2} + D{B^2}\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra AD = BC và AC = BD.
Tương tự như trên ta cũng có AB = CD.
* Chứng minh a d
a) d. Do sự bằng nhau của các tam giác ABC, CDA, BAD với tam giác DCB nên tổng các góc tại B bằng 180˚
Đối với các đỉnh còn lại cũng được lí luận tương tự như trên.
d) a. Trải các mặt ABC, ACD, ABD lên mặt phẳng (BCD).
Do tổng các góc tại B cũng như tại C, tại D đều bằng 180˚ nên các bộ ba điểm A1, C, A2; A2, D, A3; A3, B, A1là những bộ ba điểm thẳng hàng.
Như vậy, BC, CD, BD là ba đường trung bình của tam giác A1A2A3. Từ đó BD = A1C = CA2= CA. Tương tự ta cũng có AD = BC, CD = AB.
Loigiaihay.com
Bài tiếp theo
-
Câu 8 trang 121 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).
-
Câu 6 trang 120 SGK Hình học 11 Nâng cao
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABBA là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB.
-
Câu 5 trang 120 SGK Hình học 11 Nâng cao
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
-
Câu 4 trang 120 SGK Hình học 11 Nâng cao
Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng
-
Câu 3 trang 120 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :
Câu 7 trang 121 SGK Hình học 11 Nâng cao
Đề bài
Một tứ diện được gọi là gần đều nếu các cạnh đối bằng nhau từng đôi một. Với tứ diện ABCD, chứng tỏ các tính chất sau là tương đương :
a. Tứ diện ABCD là gần đều ;
b. Các đoạn thẳng nối trung điểm cặp cạnh đối diện đôi một vuông góc với nhau ;
c. Các trọng tuyến (đoạn thẳng nối đỉnh với trọng tâm của mặt đối diện) bằng nhau ;
d. Tổng các góc tại mỗi đỉnh bằng 180˚
Lời giải chi tiết
* Chứng minh a b
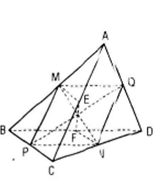
Gọi M, N, P, Q, E, F lần lượt là trung điểm của AB, CD, BC, AD, AC, BD.
a b. Do AC = BD nên MNPQ là hình thoi, vì thế MN PQ. Tương tự ta có MN EF, PQ EF.
b) a. MPNQ là hình bình hành mà MN PQ nên MPNQ là hình thoi, tức là MP = MQ, từ đó AC = BD.
Tương tự như trên, ta cũng có BC = AD, AB = CD.
* Chứng minh a c
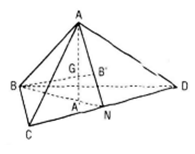
Gọi A, B lần lượt là trọng tâm của các tam giác BCD và ACD.
a) c. Ta có ΔBCD = ΔADC (c.c.c) nên BN = AN, từ đó AN = BN.
Vậy ΔAAN = ΔBBN (c.g.c), suy ra AA = BB.
Tương tự như trên, ta có điều phải chứng minh.
c) a. Do giả thiết ta có BB = AA, mà AA cắt BB tại G, AG = 3GA, BG = 3GB (xem BT 22, chương II, SGK), từ đó BG = AG và GA = GB. Các tam giác BGA và AGB bằng nhau nên BA = AB.
Như vậy BN = AN, mà :
\(\eqalign{ & A{C^2} + A{D^2} = 2A{N^2} + {{C{D^2}} \over 2} \cr & B{C^2} + B{D^2} = 2B{N^2} + {{C{D^2}} \over 2} \cr} \)
Do đó \(A{C^2} + A{D^2} = B{C^2} + B{D^2}\) (1)
Tương tự như trên ta có : \(C{A^2} + C{B^2} = D{A^2} + D{B^2}\,\,\left( 2 \right)\)
Từ (1) và (2) suy ra AD = BC và AC = BD.
Tương tự như trên ta cũng có AB = CD.
* Chứng minh a d
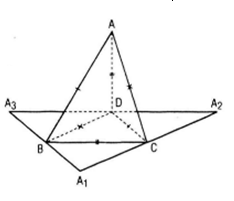
a) d. Do sự bằng nhau của các tam giác ABC, CDA, BAD với tam giác DCB nên tổng các góc tại B bằng 180˚
Đối với các đỉnh còn lại cũng được lí luận tương tự như trên.
d) a. Trải các mặt ABC, ACD, ABD lên mặt phẳng (BCD).
Do tổng các góc tại B cũng như tại C, tại D đều bằng 180˚ nên các bộ ba điểm A1, C, A2; A2, D, A3; A3, B, A1là những bộ ba điểm thẳng hàng.
Như vậy, BC, CD, BD là ba đường trung bình của tam giác A1A2A3. Từ đó BD = A1C = CA2= CA. Tương tự ta cũng có AD = BC, CD = AB.
Loigiaihay.com
Bài tiếp theo 
-
Câu 8 trang 121 SGK Hình học 11 Nâng cao
Cho tứ diện ABCD. Cắt tứ diện đó theo các cạnh đó theo các cạnh AB, AC, AD và trải các mặt ABC, ACD, ADB lên mặt phẳng (BCD) (xem hình 133). Hình phẳng gồm các tam giác BCD, A1BC, A2CD, A3BD gọi là hình khai triển của tứ diện ABCD trên mặt phẳng (BCD).
-
Câu 6 trang 120 SGK Hình học 11 Nâng cao
Cho hình lăng trụ đứng ABC.ABC có đáy ABC là tam giác vuông tại đỉnh C, CA = a, CB = b ; mặt bên ABBA là hình vuông. Gọi P là mặt phẳng đi qua C và vuông góc với AB.
-
Câu 5 trang 120 SGK Hình học 11 Nâng cao
Cho tứ diện OABC có OA, OB, OC đôi một vuông góc với nhau và OA = a, OB = b, OC = c. Gọi H là hình chiếu của O trên mặt phẳng (ABC). Tính diện tích các tam giác HAB, HBC và HCA.
-
Câu 4 trang 120 SGK Hình học 11 Nâng cao
Tam giác ABC vuông có cạnh huyền BC nằm trong mp(P), cạnh AB và AC lần lượt tạo với mp(P) các góc β và γ. Gọi α là góc tạo bởi mp(P) và mp(ABC). Chứng minh rằng
-
Câu 3 trang 120 SGK Hình học 11 Nâng cao
Cho hình chóp S.ABCD có đáy là hình vuông cạnh a, SA (ABCD). Hai điểm M và N lần lượt thay đổi trên cạnh CB và CD, đặt CM =x, CN = y. Tìm hệ thức liên hệ giữa x và y để :